1) Из (2) и (3) следует, что  .
.
2) Из (8) следует, что или 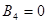 , или
, или  . Поскольку
. Поскольку 
 , то получаем
, то получаем 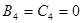 . Тогда
. Тогда  . Знак минус соответствует повороту осей на 1800, и вследствие изотропности пространства это не имеет физического смысла. Выбираем
. Знак минус соответствует повороту осей на 1800, и вследствие изотропности пространства это не имеет физического смысла. Выбираем 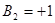 .
.
3) Поскольку в уравнения (6)-(10) входят справа или 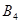 , или
, или 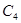 , то они удовлетворяются тождественно и интереса не представляют.
, то они удовлетворяются тождественно и интереса не представляют.
Осталось три уравнения:

Из уравнения (5) находим: 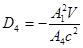 .
.
Подставляем в (4):
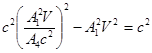 Þ
Þ 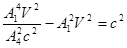 Þ
Þ 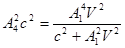 .
.
Полученное подставляем в (1):
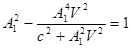 Þ
Þ 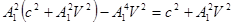 Þ
Þ
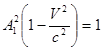 Þ
Þ 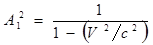 Þ
Þ
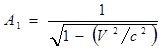 (знак плюс выбираем из физических соображений – изотропия пространства).
(знак плюс выбираем из физических соображений – изотропия пространства).
Отсюда сразу находим закон преобразования пространственных координат:
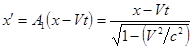 ;
; 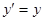 ;
; 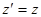 .
.
Подставляем значение 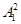 в уравнение (4):
в уравнение (4):
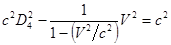 .
.
Делим на  и находим
и находим  :
:
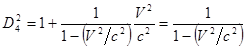 Þ
Þ
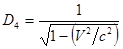 .
.
Подставляем полученное значение 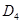 и А1 в ранее полученное выражение (5) и находим
и А1 в ранее полученное выражение (5) и находим 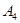 :
:
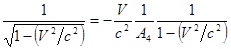 Þ
Þ
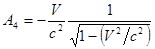 .
.
Находим закон преобразования временной координаты:
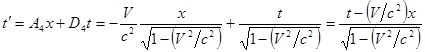 .
.
Итак, получены преобразования Лоренца:
K  K’ K’
| K’  K K
|

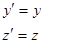
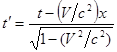
| 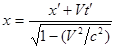


|
Обычно вводят обозначения 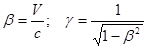 . Тогда:
. Тогда:
K 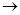 K’ K’
| K’ 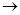 K K
|
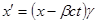

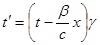

| 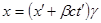
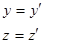
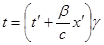
|
Преобразования Лоренца обеспечивают инвариантность уравнений Максвелла при переходе от одной ИСО к другой.
При 
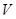 «
« преобразования Лоренца переходят в преобразования Галилея (
преобразования Лоренца переходят в преобразования Галилея (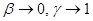 ), т. е. удовлетворяют принципу соответствия.
), т. е. удовлетворяют принципу соответствия.
| Примечание Уравнение Шредингера неинвариантно относительно преобразований Лоренца |
Следствия из преобразований Лоренца
Следствие 1
Относительность длины
Рассмотрим некоторую линейку (масштаб), неподвижную в движущейся системе отсчета  .
.

РИС. 4п-1
Длина этой линейки в системе  :
:
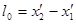 ,
,  - так называемая собственная длина линейки.
- так называемая собственная длина линейки.
Какова длина этой же линейки в системе 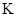 , т.е. какую длину этой линейки измерит наблюдатель, находящийся в неподвижной системе отсчета
, т.е. какую длину этой линейки измерит наблюдатель, находящийся в неподвижной системе отсчета 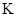 ?
?
Воспользуемся преобразованиями Лоренца:
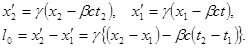
Положения концов линии - это события, поэтому в системе  нужно задать координаты событий:
нужно задать координаты событий:
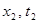 - положение одного конца линейки,
- положение одного конца линейки,
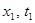 - положение другого конца линейки.
- положение другого конца линейки.
Величина 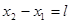 может считаться длиной линейки (масштаба) в том, и только в том случае, если пространственные координаты обоих концов определяются одновременно, т.е.
может считаться длиной линейки (масштаба) в том, и только в том случае, если пространственные координаты обоих концов определяются одновременно, т.е. 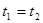 , или
, или 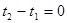 .
.
Рассмотрим это положение подробнее. Для этого разберем пример.
Пример
 Измерение длины движущегося поезда.
Измерение длины движущегося поезда.
РИС. 4п-2
1) Собственную длину  измеряем непосредственно в поезде путем протягивания мерной ленты через все вагоны и паровоз.
измеряем непосредственно в поезде путем протягивания мерной ленты через все вагоны и паровоз.
2) Измеряем длину поезда из неподвижной системы координат K.
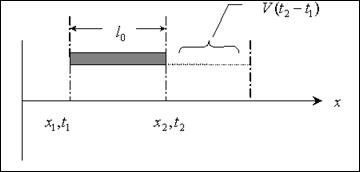 а) Пусть в момент
а) Пусть в момент 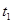 измерено положение хвоста поезда
измерено положение хвоста поезда  ; в момент времени
; в момент времени 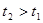 измерено положение головы поезда
измерено положение головы поезда 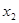 . Однако за время
. Однако за время 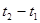 поезд прошел расстояние
поезд прошел расстояние  . Поэтому кажущаяся его длина в неподвижной системе отсчета
. Поэтому кажущаяся его длина в неподвижной системе отсчета  .
.
РИС. 4п-3
б) Другая последовательность измерений.
Пусть в момент 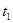 фиксируется положение головы поезда
фиксируется положение головы поезда 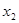 , в момент времени
, в момент времени  фиксируется положение хвоста поезда
фиксируется положение хвоста поезда 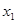 .
.
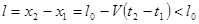 .
.
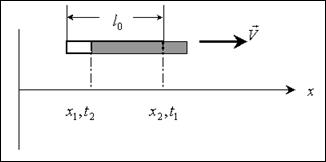
РИС. 4п-4
Если интервал, промежуток времени 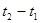 , достаточно велик, то можно получить абсурдный результат
, достаточно велик, то можно получить абсурдный результат 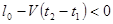 .
.
Общий вывод
Пространственной длиной масштаба (или просто длиной масштаба) называется величина  при условии, что пространственные координаты концов его определялись одновременно.
при условии, что пространственные координаты концов его определялись одновременно.
Итак, длина масштаба, измеренная из неподвижной системы отсчета при условии 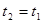 :
: 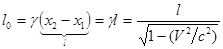 Þ
Þ
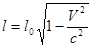
|
Длина масштаба  в системе
в системе  в направлении движения меньше его собственной длины
в направлении движения меньше его собственной длины  в системе
в системе 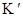 . Это явление называется лоренцовым сокращением длины.
. Это явление называется лоренцовым сокращением длины.
Поскольку сокращение происходит только в направлении движения тела, его объем есть 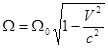 .
.
Движущееся тело сплющивается в направлении движения.
| Вывод Длина, линейный размер, объем не являются понятиями абсолютными, они относительны, они зависят от того, в какой системе отсчета они измеряются. |
Следствие 2
Относительность промежутков времени
Если часы находятся в точке 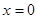 , то преобразование времени:
, то преобразование времени:
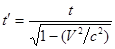 .
.
Пусть в неподвижной системе отсчета прошел некий промежуток времени: начало 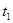 , конец
, конец  , интервал
, интервал  .
.
Тогда в движущейся системе отсчета:
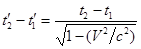 .
.
Поскольку 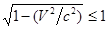 , то всегда
, то всегда 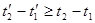 .
.
 2020-10-10
2020-10-10 99
99








