Общая процедура составления и решения системы уравнений

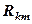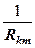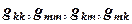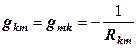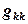Если элемент соединяет два узла и , то параметр , а точнее,  входит в четыре коэффициента матрицы: , причем , а в  и 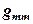параметр  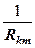входит в виде слагаемого. Алгоритм составления системы уравнений таков:

1) Обнуляем матрицу и правую часть: .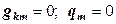

2) Обходим по очереди все элементы. Для каждого определяем 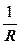 и добавляем (суммируем) это число к четырем коэффициентам матрицы: к двум - с плюсом, а к двум другим - с минусом. Аналогичную процедуру проводим с правой частью.

3) Матрица составлена, применяем к ней решение методом Гаусса.

4) Если это не первая итерация, то пробуем ускорить сходимость, используя предыдущие итерации.

5) Оцениваем невязку и переходим к следующей итерации или считаем решение окончательным.

В ходе итераций требуется многократное решение одной и той же системы уравнений, но с различными правыми частями.

Возможны два варианта:

1) Полное обращение матрицы :

.

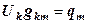
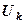После этого можно подставлять любые новые  и сразу получать , но операция обращения требует б о льших вычислительных затрат, чем решение системы методом Гаусса (примерно во столько раз, сколько в системе неизвестных).

2) Применение метода Гаусса. В этом случае на каждой итерации сохраняются два прохода - прямой и обратный, но только для правой части.