Возможны два пути применения итераций при решении системы уравнений.
I. Итерационное решение системы уравнений (применяется вместо метода Гаусса). Порядок итераций такой (см. схему на рис. 12.3):
1) Задаемся начальными значениями потенциала в точках 1, 2, 3 …, например 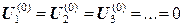 (кроме А, В,…, в которых потенциал известен).
(кроме А, В,…, в которых потенциал известен).
2) Проводим итерационное уточнение значений потенциала, для этого обходим по очереди все точки модели:
- у точки 1 в уравнение постоянства заряда входят значения в точках со второй по пятую; поскольку все они имеют нулевой потенциал, значение в точке 1 после первой итерации не изменится: 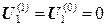 ;
;
- у точки 2 среди соседей есть точки A и B, потенциалы которых 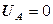 и
и  известны, а
известны, а 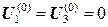 , по этим данным из уравнения постоянства заряда можно найти
, по этим данным из уравнения постоянства заряда можно найти 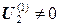 ;
;
- пройдя по остальным точкам, убедимся, что в них потенциал не изменится: 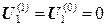 .
.
3) Теперь будем считать  новыми значениями в т. 1, 2, 3 и повторим итерационное уточнение значений потенциала:
новыми значениями в т. 1, 2, 3 и повторим итерационное уточнение значений потенциала:
- в точке 1 потенциал изменится 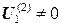 , поскольку на предыдущей итерации изменился потенциал в смежной с ней точке 2;
, поскольку на предыдущей итерации изменился потенциал в смежной с ней точке 2;
- в точке 2 потенциал не изменится 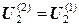 , поскольку на предыдущей итерации не изменялся потенциал в смежных с ней точках A, B, 1 и 3;
, поскольку на предыдущей итерации не изменялся потенциал в смежных с ней точках A, B, 1 и 3;
- из остальных точек потенциал изменится в точке 3 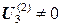 , поскольку на предыдущей итерации изменился потенциал в смежной с ней точке 2.
, поскольку на предыдущей итерации изменился потенциал в смежной с ней точке 2.
4) Такой перебор всех точек будем повторять, пока хотя бы в одной из них будет происходить изменение потенциала. Итерации прекращаются, когда эти изменения за итерацию станут меньше заданного уровня точности 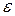 :
:
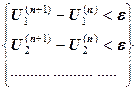
Достоинствами этого метода являются простота (уравнения составляются и решаются поочередно, полная система уравнений не составляется) и устойчивая сходимость при любом числе неизвестных. Его недостаток необходимость многократных обходов и медленная сходимость (особенно вначале, если исходное приближение выбрано неудачно).
Разновидностью данного метода является метод Зейделя, в котором применение найденных значений неизвестных производится сразу, а не со следующей итерации.
II. Итерационное уточнение решения, полученного методом Гаусса. Чтобы организовать итерационный процесс, нужно представить искомое значение на итерации в виде суммы значения на предыдущей итерации и приращения за итерацию:
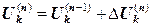 . (12.12)
. (12.12)
Подставив это выражение в систему уравнений (12.7), получим:
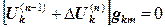 ;
;
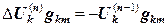 . (12.13)
. (12.13)
Это система уравнений относительно  , аналогичная (12.7), но с правой частью. Выражение в правой части представляет собой невязку (погрешность) после предыдущей итерации.
, аналогичная (12.7), но с правой частью. Выражение в правой части представляет собой невязку (погрешность) после предыдущей итерации.
Ход итерационного процесса такой:
1) Задаемся начальными значениями потенциала 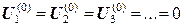 .
.
2) Находим из решения системы (12.13) 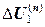 , затем
, затем  по формуле (12.12).
по формуле (12.12).
3) Если после подстановки этих значений в исходные уравнения (12.7) получаем тождества, то найденные значения являются точными, и итерации прекращаются. Если же невязка 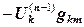 ненулевая, то выполняется следующая итерация. Невязка от предыдущей итерации оказывается в правой части уравнений (12.13), и мы ищем такую добавку к значениям неизвестных
ненулевая, то выполняется следующая итерация. Невязка от предыдущей итерации оказывается в правой части уравнений (12.13), и мы ищем такую добавку к значениям неизвестных 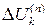 , чтобы она скомпенсировала невязку от предыдущей итерации. Суммируя предыдущее решение с этой добавкой, находим новое приближение по формуле (12.12).
, чтобы она скомпенсировала невязку от предыдущей итерации. Суммируя предыдущее решение с этой добавкой, находим новое приближение по формуле (12.12).
4) Условием завершения итераций является уменьшение до заданного порога либо невязки 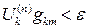 , либо приращения за шаг
, либо приращения за шаг 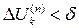 .
.
 2020-10-10
2020-10-10 186
186








