Изопараметрическое преобразование при построении КЭ

Существуют следующие виды КЭ:

- субпараметрические – элементы, в которых полиномы, описывающие внутреннее состояние элемента (температуру, перемещения), имеют порядок ниже, чем описывающие геометрическую форму элемента;

- изопараметрические (наиболее распространенные) - позволяют использовать одинаковые функции при построении элемента и при работе с ним;

- суперпараметрические - элементы, в которых внутреннее состояние элемента описывают полиномы более высокого порядка.

Каждая из функций формы (ФФ) конечного элемента обращается в единицу в одном из его узлов и в нуль – в остальных, при этом в каждой точке КЭ сумма всех ФФ равна единице. Для квадратичного элемента сложной формы с большим количеством узлов вывести уравнения для таких функций непросто. Выход в том, что уравнения составляют для простого элемента, который является моделью сложного.

Рассмотрим пример четырехугольного элемента с восемью узлами (рис. 12.29).

Рис. 12.29. Изопараметрическое преобразование: А – КЭ, В – его модель.

 

На рис. 12.29 справа изображен элемент А в глобальной системе координат , а слева – его модель В в локальных координатах . Начало локальных координат – в центре элемента, диапазон их изменения от -1 до 1. Модель имеет вид квадрата размером 2х2, все локальные координаты узлов равны -1, 0 или 1. Стороны самого конечного элемента являются квадратными параболами, координаты всех восьми узлов могут быть любыми.

Вначале обеспечим условия равенства нулю. ФФ  для узла 2 должна быть равна нулю в точках 1, 3, 4, 5, 6, 7 и 8. Это можно обеспечить, задав  в виде произведения трех функций: . Первая из них обращается в нуль в узлах 1, 7, 8, вторая - в узлах 3, 4, 5, а третья в узлах 5, 6, 7.

Подставив координаты узла 2: , получим . Значит, формулу нужно изменить: . Аналогично:

, , .

Для угловых узлов функции немного другие:

, ,

, .

Эти ФФ будут годны не только для модели, но и для самого КЭ, если мы найдем способ установить однозначное соответствие между точками элемента и его модели. 

Переход от В к А простой. Если даны локальные координаты 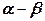 точки модели В, то можно найти значения ФФ для этой точки и вычислить глобальные координаты точки А по формулам:

, , .                         (12.112)

Если точка В совпадает с одним из узлов, например, с узлом 3, то для нее , а остальные ФФ равны нулю. Тогда, согласно (12.112), координаты точки А совпадут с координатами  точки 3.

Обратный переход от А к В гораздо сложнее, поэтому весь алгоритм устроен так, чтобы переходить только от В к А. Перейти от А к В достаточно просто в случае одномерного (стержневого) квадратичного элемента.

Изопараметрическое преобразование можно использовать для разбиения построенного КЭ на более мелкие. Разбиение производят на модели КЭ, а затем по локальным координатам узлов полученных мелких элементов рассчитываются глобальные координаты этих узлов.

Чтобы обеспечить стыковку создаваемых сеток в смежных элементах, целесообразно вначале разбить на части их общие ребра, затем общие грани между ребрами, а затем уже - внутренние объемы между гранями.

Разбиение пространственных искривленных пластин производится так же, как и разбиение плоских пластин. Модель остается прежней (см. рис. 12.29), ФФ вычисляют по тем же формулам, но каждый узел КЭ имеет три глобальных координаты , и изопараметрическое преобразование осуществляется по формулам:

, , , .                   (12.113)

Этот подход может быть распространен на разбиение объемного КЭ. Вначале разбиваем ребра, размещая на них дополнительные узлы. Затем разбиваем грани. Поскольку на ребрах по контуру грани все узлы размещены, эта задача сводится к разбиению пространственной пластины. После этого на каждой грани появляются линии сетки с узлами на них. Четыре такие линии, по одной с каждой грани, образуют четырехугольник, который можно разбить таким же образом, как и грань.

Для расчета деформаций необходимо вычисление градиентов (производных функций формы по одной из координат):

.      (см. (12.97))

Поскольку ФФ выражена в локальных координатах , ее производная по глобальной координате :

,                                                (12.114)

где  – градиент для модели элемента;  – якобиан (матрица Якоби, матрица искажения пространства). Если модель полностью совпадает с элементом, то , если она отличается от него только масштабным множителем, то . Если же элемент криволинейный, то в каждой его точке своя матрица перехода размером  (для плоского КЭ)

                                                  (12.115)

или  (для объемного КЭ). Чтобы вычислить якобиан, нужно составить матрицу , а затем найти обратную матрицу . Весь алгоритм построен так, что мы двигаемся только от В к А (см. рис. 12.29).