| Расчет t-критерия Стьюдента | Пример |
I. Формула расчета: 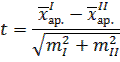 | Представлен в табл. 1. |
II. Находим среднее арифметическое значение для каждой выборки по формуле:  | Находим среднее арифметическое значение для каждой группы: 2.1.    2.2. 2.2.    |
| III. Находим отклонение каждого количественного показателя от среднего арифметического и квадрат отклонения для каждой выборки. | 3.1.  : (столбец 3) 3.2. : (столбец 3) 3.2.  : (столбец 7) 3.3. : (столбец 7) 3.3.  (столбец 4) (столбец 4)  (столбец 8) (столбец 8) |
IV. Находим отдельно сумму квадратов отклонений для двух выборок по формуле:  | Определяем сумму квадратов отклонений для: 4.1. первой группы (n1)  4.2. второй группы (n2) 4.2. второй группы (n2)  |
V. Находим σ – стандартное отклонение в каждой выборке по формуле:  | 5.1. Находим σ – стандартное отклонение в первой группе (n1):  5.2. Находим σ – стандартное отклонение во второй группе (n2): 5.2. Находим σ – стандартное отклонение во второй группе (n2):  |
VI. Находим ошибку средней в каждой группе по формуле: 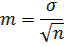 | 6.1. Находим ошибку средней для первой группы (n1):  6.2. Находим ошибку средней для второй группы (n2): 6.2. Находим ошибку средней для второй группы (n2):  |
VII. Находим значения t-критерия Стьюдента по формуле: 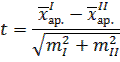 |    t = 2,65 t = 2,65 |
VIII. Находим число степени свободы по формуле:  где n – количество испытуемых в обеих выборках. где n – количество испытуемых в обеих выборках. | Число степени свободы:   |
| IX. По таблице «Критические значения t-критерия Стьюдента» по числу степени свободы V определить уровень статистической значимости (достоверности) (p ≤ 0,05; p ≤ 0,01). |    |
| X. Вывод о статистической значимости (достоверности) различий двух средних арифметических значений изучаемого психологического признака, полученных в двух выборках. | Принимается гипотеза H1, т.е., скорость чтения в первой группе испытуемых достоверно превышает скорость чтения во второй группе испытуемых (p<0,05) |
Таблица 2.1
Критические значения t (критерия Стьюдента)
| К | Доверительные уровни | К | Доверительные уровни | ||||
| 95% | 99% | 99,9% | 95% | 99% | 99,9% | ||
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | 12,71 4,30 3,18 2,78 2,57 2,45 2,37 2,31 2,26 2,23 2,20 2,18 2,16 2,15 2,13 2,12 2,11 2,10 2,09 2,09 | 63,86 9,93 5,84 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,06 3,01 2,98 2,95 2,92 2,90 2,88 2,86 2,85 | 636,6 31,60 12,94 8,61 6,86 5,96 5,41 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,02 3,97 3,92 3,88 3,85 | 21 22 23 24 25 26 27 28 29 30 40 50 60 80 100 120 200 500 ¥ | 2,08 2,07 2,07 2,06 2,06 2,06 2,05 2,05 2,04 2,04 2,02 2,01 2,00 1,99 1,98 1,98 1,97 1,96 1,96 | 2,83 2,82 2,81 2,80 2,79 2,78 2,77 2,76 2,76 2,75 2,70 2,68 2,66 2,64 2,63 2,62 2,60 2,59 2,58 | 3,82 3,79 3,77 3,75 3,73 3,71 3,69 3,67 3,66 3,65 3,55 3,50 3,46 3,42 3,39 3,37 3,34 3,31 3,29 |
| К | 5% | 1% | 0,1% | К | 5% | 1% | 0,1% |
| Уровни значимости | Уровни значимости | ||||||
Способ применения таблицы. К – число степеней свободы. Его находят по формуле n 1 + n 2 – 2, где n 1 и n 2 – число наблюдений в сравниваемых выборках.
ЛЕКЦИЯ 10
Метод характеристических интервалов
Сущность математического анализа по способу В. С. Генеса заключается в том, чтобы для признаков имеющих качественное выражение (различные значения психологических признаков), определить частоту (процент и ошибку) и сравнивать эти частоты между собой для определения достоверности различий.
Метод характеристических интервалов позволяет определить чувствительность различных качественных значений психологического признака по проценту и его ошибке, полученных в каждой группе (выборке), для установления достоверности различий между ними.
Метод характеристических интервалов позволяет выявить достоверность различных значений психологического признака (например, высокий, умеренный, низкий уровень) между двумя выборками (группами).
 2020-10-10
2020-10-10 849
849








