Основные свойства степенных рядов

1) Во всех точках, лежащих внутри интервала сходимости, сумма степенного ряда является непрерывной функцией переменной x:

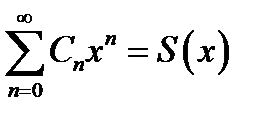
2) Степенной ряд можно почленно интегрировать внутри интервала сходимости:

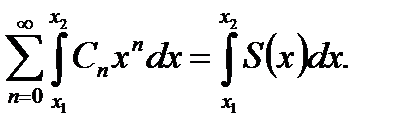
3) Внутри интервала сходимости степенной ряд можно почленно дифференцировать:

При почленном интегрировании и дифференцировании степенных рядов их интервалы сходимости не меняются.

Пример. Найти сумму ряда

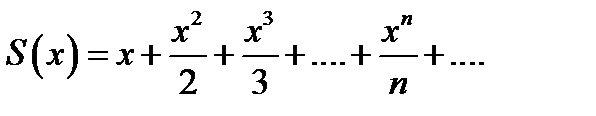                                                            (7.21)

Решение. Найдем сначала интервал сходимости этого ряда

Следовательно, интервал сходимости ряда (-1, +1). Продифференцировав (7.21), имеем

S ¢(x) = 1 + x + x ² +... + xⁿ  +....

Правая часть этого выражения - геометрический ряд с q = x, который сходится при ½ x ½<1. Поэтому, используя формулу суммы сходящейся геометрической прогрессии, получим

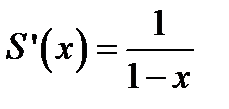
Отсюда сумму исходного ряда найдем интегрированием

Найдем C. Из (7.21) следует, что S (0) = 0. Следовательно,

 0 = - ln (1-0) + C, C = 0.

Таким образом, S (x) = - ln (1- x) = .

 

Ряды по степеням (х - а). Наряду со степенными рядами относительно переменной х часто рассматривают степенные ряды по переменной (x - a), т. е. ряды вида

 

C ₀ + C ₁(x - a) + C ₂(x - a)² +... + C_n (x -a) ⁿ +...                                  (7.22)

                                                  

Очевидно, что этот ряд подстановкой y = (x - a) превращается в ряд типа (7.18). Поэтому, если степенной ряд (7.18 имеет интервал сходимости 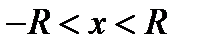, то соответствующий ряд вида (7.22) имеет интервал сходимости 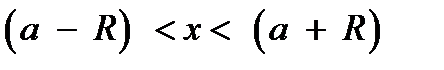, центр которого расположен в точке x = a.

Пример. Найти интервал сходимости следующего ряда

 

 

Решение. Найдем радиус сходимости ряда. В соответствии с (7.20) имеем

 

 

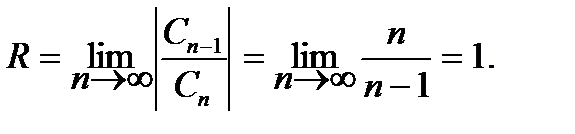
Отсюда -1 < (х ³ -1) < 1 или 0 < x ³  < 2.

Следовательно, интервал сходимости ряда 0 < x < .

 

Ряд Тейлора. Пусть функция f (x) в точке х = а имеет производные любого порядка. Предположим, что имеется сходящийся степенной ряд

C ₀ + C ₁(x - a) + C ₂(x - a)² +... + C_n (x -a) ⁿ +   =               (7.23)

сумма которого равна функции f (x), т. е.

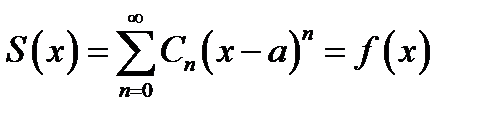.                                                                      (7.24)

Найдем коэффициенты такого ряда. Очевидно, что f (a) = C ₀. Продифференцировав (7.24) в точке   х=а, имеем C ₁ = f ¢(a). Продифференцировав (7.24) в точке х=а дважды, получим C ₂ = f¢¢(a)/2. Продолжая дифференцирование равенства (7.24) в точке х = а, можно убедится, что коэффициенты ряда (7.23) находятся по формуле

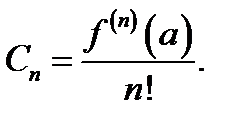
Степенной ряд вида

называется рядом Тейлора  для функции f (x).

Теорема. Для того чтобы бесконечно дифференцируемая функция f (x) являлась суммой составленного для нее ряда Тейлора, необходимо и достаточно, чтобы остаточный член в формуле Тейлора (2.25) стремился к нулю при n ® ¥.

Если для всех значений x из некоторой окрестности точки х = a имеет место равенство

 

 

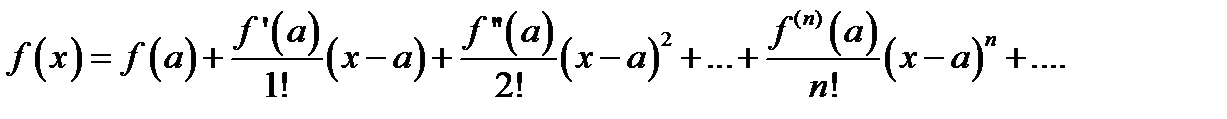
то функция f (x) называется разложимой в ряд Тейлора в окрестности точки x = a (или по степеням (x - a)).

В частном случае при a = 0 ряд Тейлора имеет вид

 

f (x) =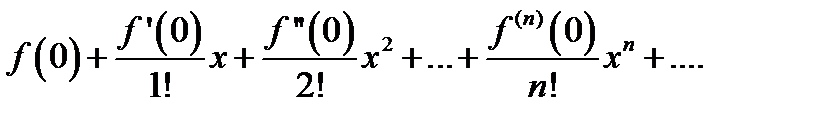

 

и его называют рядом Маклорена.

Пример 1. Разложить в ряд Тейлора функцию f (x) = e^x.

Поскольку e^x =(e^x)¢=(e^x)¢¢ =...(e^x)⁽ⁿ⁾, то при x = 0 f (0) = 1; f ¢(0) = 1; f ¢¢(0) = 1;...; f ⁽ⁿ⁾(0) = 1;....

Следовательно, ряд Тейлора функции y = e^x в окрестности точки x = 0 имеет вид

e^x = 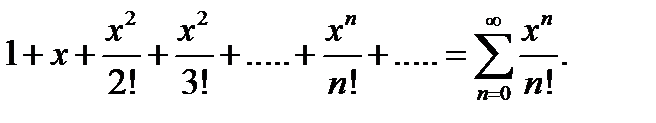                                               (7.25)

Ряд (7.25) сходится на всей числовой оси к функции y = e^x.

Пример 2. Разложить в ряд Тейлора функцию f (x) = sin x.

Решение. Для функции f (x) = sin x имеем:

 

, ,… .

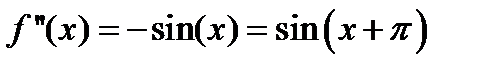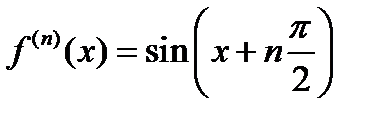Следовательно, ряд Тейлора для sin x:

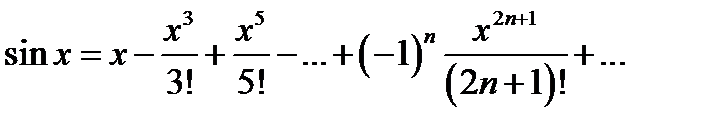
или

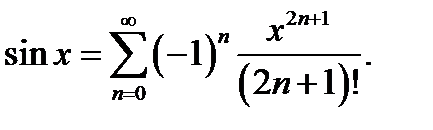
Аналогично получается разложение для функции cos x:

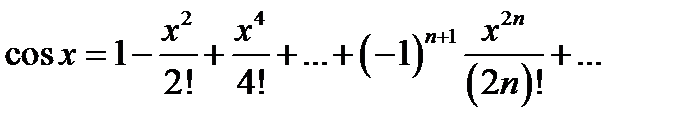
или

cos x = .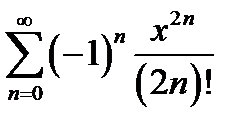

Подобным образом можно получить разложения в ряд Тейлора и многих других функций.

 

 

Теоpия веpоятности.

4.1. Элементы комбинаторики.

 

Основной задачей комбинаторики является определение числа подчиненных тем или иным правилам комбинаций (наборов или соединений), которые можно составить из заданного множества (набора) объектов. Природа элементов, входящих во множество, может быть любой, например, какие-то предметы, или люди, или числа и т. п.

Итак, пусть задано множество A из n объектов 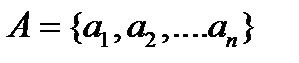. Последовательность произвольных элементов { a ₁, a ₂,..., a_r } называется выборкой объема r из исходного множества A. В комбинаторике выборку называют соединением. Возможны следующие варианты: объект может выбираться только один раз, т. е. после выбора он назад не возвращается, или несколько раз: это означает, что объект выбирается и потом снова возвращается в исходное множество. В последнем случае объем выборки может превосходить объем исходного множества A. Далее, если свойства выборки изменяются при перемене местами двух элементов, то выборка называется упорядоченной, в противном случае - неупорядоченной. Число появлений одного и того же элемента a _i  называется его кратностью и обозначается m (a). Типичным примером выборки является слово.

Две основные задачи, рассматриваемые в теории соединений:

а) составление всех соединений данного вида;

б) расчет количества всех возможных соединений данного вида.

Для решения первой задачи используются следующие правила.

Правило суммы (правило сложения):

Если объект А можно выбрать из некоторого набора элементов m способами, а объект В – n способами, то осуществить выбор объекта А или В можно m + n способами.

Пример. Пусть а – число, делящееся на 2; b – число, делящееся на 3. Сколькими способами можно выбрать или а, или b из множества чисел .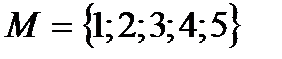

Решение. Число а можно выбрать двумя способами (2; 4), а число 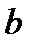 ˗ одним способом (3), тогда по правилу суммы .

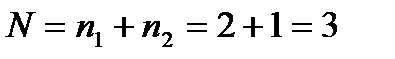Правило произведения (умножения):

Если объект А можно выбрать m способами, а объект В – n способами, то выбор пары (А, В) можно осуществить m 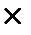 n способами.

Пример. На главные роли в фильме пробуются 4 актёра М ₁, М ₂, М ₃, М ₄ и 2 актрисы W ₁ и W ₂. Известно, что М ₁ и W ₂ не подходят друг другу по росту, а М ₄ и W ₁ – психологически несовместимы. Сколько имеется вариантов состава исполнителей? 

Решение: 4 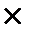 2 – 2 = 6.

Пример. Имеются цифры 0, 1, 2, 3, 4, 5. Сколько четырехзначных чисел можно составить из них?

 Решение: .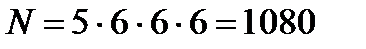

Замечание. Правила суммы и произведения можно распространять на любое число объектов.

Рассмотрим самое простое соединение. Пусть исходное множество из n элементов разбито на k групп (наборов), содержащих n ₁ , n ₂,..., n_k элементов каждая, т. е. первый набор из n₁ элементов, второй из n ₂ элементов и т.д. Сколько различных соединений можно составить, если из каждого набора надо взять только один элемент? Очевидно, что каждый элемент первого набора может встретиться в соединении с каждым элементом второго набора и таких пар будет n _{1 ∙} n ₂. Каждая такая пара может встретиться с каждым элементом третьего набора, т. е. разных троек уже будет n _{1 ∙} n_{2 ∙} n₃. Если обозначить за N число всех возможных соединений по одному элементу из каждого из k наборов, то получим

 

N = n₁ ∙ n₂ ∙... n_k.                                                                        (1.1)

 

Пример 1. В некотором городе телефонные номера состоят из буквы и пяти цифр. Буква может быть только А, В или Г. Первая цифра бывает 2, 3, 4 или 5, а остальные цифры могут быть любые. Сколько телефонов может быть установлено в этом городе?

Решение. Первый набор состоит из трех букв А, В или Г, т.е. n ₁ = 3, второй - из четырех цифр 2, 3, 4 или 5, n ₂ = 4. Следующие четыре набора содержат по 10 цифр, т.е. n ₃ = n ₄ = n ₅ = n ₆  = 10. Тогда всего различных номеров может быть N = 3 ´ 4 ´ 10 ´ 10 ´ 10 ´ 10 = 120 000.

В частном случае, если все k наборов содержат одинаковое количество элементов m, то

 

N = m^k                                                                                  (1.2)

 

Пример 2. Бросают две игральных кости. Сколько различных пар чисел может выпасть? (Нужно учесть, что 1 на первой кости и 2 на второй или 2 на первой и 1 на второй - это разные пары, т. е. разные соединения, что легко увидеть, если кости разного цвета).

Решение. У нас k = 2. А так как у игральной кости, имеющей форму кубика, шесть граней, то m = 6, поэтому 

 

N = 6² = 36.

Соединения, рассматриваемые в комбинаторике, называются: перестановки, размещения и сочетания.

Перестановки. Перестановками из n элементов называются комбинации из n элементов, которые отличаются друг от друга только порядком расположения элементов.

Количество возможных перестановок вычисляется по формуле

 

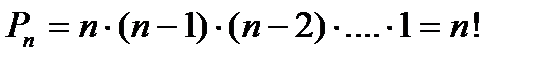                                                   (1.3)

 

Действительно:

1-й элемент можно выбрать n – способами;

2-й – (n - 1) способами;

3-й – (n - 2) способами … и т.д.

По правилу произведения получим 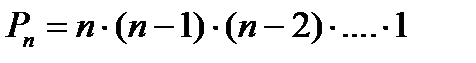. Такое произведение обозначается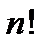

Пример 1. Сколькими способами можно расставить 5 судов у причальной стенки?

Решение. Р ₅ = 5! = 120

Пример 2. Имеются карточки с буквами ДРУГ. Сколько «слов» можно составить из этих букв? 

Решение. .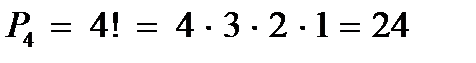

Размещения. Название “размещение” произошло от задачи: разместить k предметов в n пронумерованных ячейках. Размещением из n  элементов по k  элементов называются комбинации из k элементов, которые отличаются друг от друга составом элементов и (или) порядком их расположения. Формула размещения k элементов по n ячейкам:

 

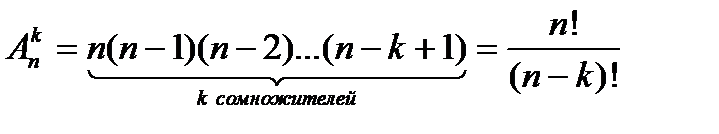                                                     (1.4)

Пример 1. Элементы а,в, с разместить по два элемента.

Решение. Возможно 6 вариантов 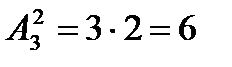. Это ав, ва, ас, са, вс, св.

Пример2. Сколько можно составить семизначных телефонных номеров, в каждом из которых ни одна цифра не повторяется?

Решение. .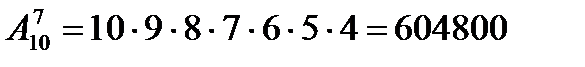

 

Сочетания. Сочетания из n -элементов по k – элементам называется комбинацией из k-элементов, которые отличаются друг от друга только составом элементов (хотя бы одним элементом).В отличие от размещения, порядок расположения элементов внутри комбинации не имеет значения. Поэтому количество комбинаций при размещении  уменьшается на количество перестановок k!

 

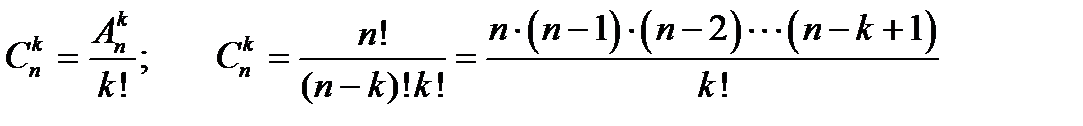.                        (1.5)

Правило симметрии: 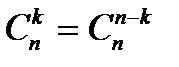. Например: .

Пример 1. В ящике 10 шаров. Сколькими способами можно достать 3 шара?

Решение. .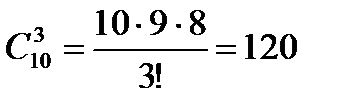

Пример 2. В розыгрыше первенства по футболу принимают участие 16 команд, при этом любые две команды играют между собой только один матч. Сколько всего календарных игр?

 

Решение. .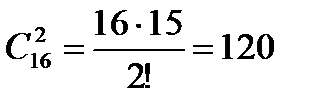

Случайные события

Основные определения. Испытанием называется осуществление на практике какого-либо комплекса условий. В теории вероятности изучаются такие испытания, которые могут быть повторены неограниченное число раз.

В результате испытания наблюдаются различные явления, которые называются событиями. Каждому проведению испытания соответствует определённый исход – событие, которое называется элементарным событием. События обозначаются заглавными латинскими буквами А, В, С …

  События подразделяются на 3категории: случайные, достоверные, невозможные.

Определение. Событие называют случайным, если при данных условиях (в данном опыте) оно может произойти, а может и не произойти по независящим от нас причинам.

  Пример 1. Бросается круглая однородная монета на твёрдую горизонтальную поверхность. Элементарные события – выпадение "орла" и "решки". Если изменить условия (бросания монеты), например, бросать на песчаном пляже, то добавляется ещё одно элементарное событие – "на ребро" (монета встаёт вертикально)

Пример 2. Испытание состоит в подбрасывании игральной кости. Игральная кость правильная, т. е. на каждой грани куба – одно из натуральных чисел от 1 до 6. Случайным событием является, например, событие «выпадение четного числа очков больше 4».

Определение. Невозможным называют событие, которое никогда не произойдёт в результате испытания. Обозначается – Ø.

Пример. Выпадение числа 8 при бросании обыкновенной игральной кости.

Определение. Достоверным событием называется то событие, которое обязательно произойдёт в результате испытания.

Пример. Выпадение целого числа от 1 до 6 при бросании игральной кости.

Замечание. Категории "невозможные" и "достоверные" события подчас зависят от условий конкретного испытания. При "нормальных" условиях бросания монеты событие "упадёт на ребро" – "невозможное" событие, а при условии бросания на песок – случайное событие.

Теперь рассмотрим ряд определений, характеризующих взаимосвязь нескольких событий, которые участвуют в одной и той же задаче. В этом смысле события подразделяются на совместные и несовместные.

Определение. Два события А и В называются совместными, если появление обоих событий возможно в данном испытании.

Например, из колоды вынимают наудачу одну карту. Событие А – появление дамы. Событие В – появление карты масти «пик». События А и В (появление карты дама-пик) совместны.

Определение. Два события А и В называются несовместными, если наступление одного из них исключает наступление другого.

Пример 1. Событие А – выпадение «орла» при одном бросании монеты, событие В – выпадение «решки». Эти события несовместны.

Пример 2. Событие А – выпадение на кости числа очков больше 5. Событие В – выпадение числа очков менее 3.

Определение. События А ₁, А ₂, …, А_n составляют полную группу, если в результате испытания произойдёт одно и только одно из них.

Пример. В урне 1 белый шар, 2 зеленых и 3 красных. Вынимают наудачу один  шар. События А – вынутый шар белый; В – вынутый шар зеленый и С – красный составляют полную группу событий.

Определение. События А ₁, А ₂, …, А_n равновозможными, если в силу равенства или симметрии или однородности, никакие из них нельзя выбрать как происходящие чаще других при многократном повторении опыта.

Пример. При бросании игральной кости выпадение от 1 до 6 очков является равновозможными событиями в силу однородности и симметричности игральной кости (кубика).

Определение. События, образующие полную группу попарно несовместных и равновозможных событий, называются исходами (случаями, элементарными событиями). Таким образом, все исходы – это множество всех равновозможных и единственно возможных событий.

Например, при подбрасывании монеты ˗ 2 исхода, при подбрасывании игральной кости – 6 элементарных исходов.

Определение. Исходы, которые влекут за собой появление событий А, называются благоприятными событию А.

Например, если событие А – при одном бросании игральной кости выпало число очков, кратное 3, то из шести возможных исходов благоприятными событию А являются два исхода: появление 3 и 6 очков, а событию В – появление четного числа очков – благоприятны три исхода из тех же шести.

 

Понятие вероятности

«Классическое» определение вероятности. Рассмотрим опыт (эксперимент), в результате которого может произойти «п» исходов (напомним, что исход – это равновозможные несовместные попарно события, образующие полную группу событий).

Вероятностью случайного события называется число, равное отношению числа исходов  т, благоприятных этому событию, к общему числу исходов п в данном опыте.

 

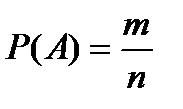                                                                                                  (3.1)

 

Эта формула называется классической формулой для вычисления вероятностей. Вероятность события А обычно обозначается Р (А). Очевидно, что

 

.

 

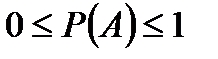Невозможному событию присваивается вероятность, равная нулю. Достоверному событию – вероятность, равная единице.

Пример 1. В коробке находятся 10 шаров. 3 из них ˗ красные, 2 – зеленые, остальные  ˗ белые. Найти вероятность того, что вынутый наугад шар будет: а) красным, б) зеленым, в) белым.

Появления красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара – событие А, появление зеленого – событие В, появление белого – событие С.

Тогда, по формуле (10.8), получаем:

 

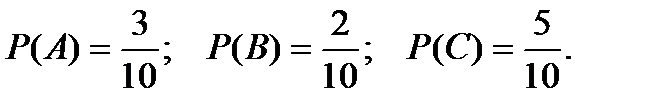
Пример 2. Есть два друга К и В. Какова вероятность, что К и В окажутся рядом за круглым столом, вмещающим 10 человек, причем К окажется справа от В?

Решение. Пусть событие А - К и В окажутся рядом, причем К окажется справа от В. Общее число исходов можно найти как число размещений из 10 элементов по 2: 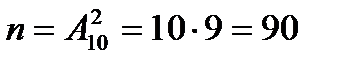; число благоприятствующих событию А исходов 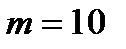(1 и 2 место, 2 и 3, и т. д. до 10 и 1)

 

.     

             

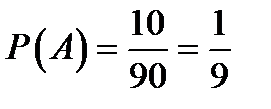Замечание: при использовании классического определения вероятности используют формулы комбинаторики.

Статистическая вероятность. Рассмотрим пример: пусть в урне 10 одинаковых по размеру шаров, но два из них ˗ белые, три ˗ черные и пять ˗ красные. Опыт заключается в том, что вынимают наугад один шар. При этом шар может оказаться или белым, или черным, или красным. Будем в каждом опыте вытаскивать шар, фиксировать его цвет, а затем возвращать его в урну. После перемешивания опыт повторяется. Пусть проведено п таких опытов. В  результате, белый шар вынимался 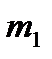 раз, красный 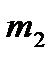, а черный  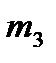раз. Частота появления каждого из возможных событий есть отношение .

В общем случае частотой появления события А в п опытах называется отношение числа появления этого события т к числу проведенных опытов п.

Если проводить такой опыт значительное число раз, то окажется, что примерно в половине случаев вынули красный шар, в двадцати процентах случаев – белый, в тридцати – черный. По мере увеличения числа опытов соотношение шансов возможных событий 5: 2: 3 соответственно, будет подтверждаться все с большей точностью. Поэтому статистическая вероятность вычисляется по формуле

 

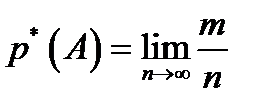                                                                              (3.2)

 

Введенная таким образом вероятность событий носит название статистической или априорно-частотной.

Известны опыты, проводившиеся Бюффоном (XVIII в.) и Пирсоном (XIX в.), когда при 4040 подбрасываниях монеты относительная частота появления герба оказалась равной 0,506 9, а при 23 000 подбрасываниях (Пирсон) - 0,500 5, т. е. практически не отличалась от вероятности этого события, равной 0, 5.