Основные свойства функции плотности вероятности

1. Функция плотности вероятности - неотрицательная возрастающая функция, f (x) ³ 0.

2. Интеграл от 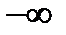 до 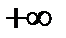 от функции плотности вероятности (если она задана на всей числовой оси) равен 1. Действительно, как частный случай формулы (12.10) имеем

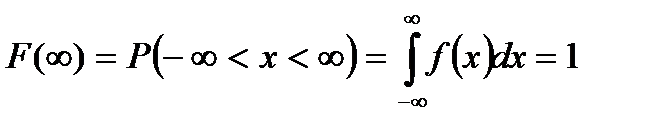.                                           (5.9)

З амечание. Если случайная величина задана только на отрезке [а, b), то в формуле (5.9) пределы интегрирования изменяются на a и b.

 

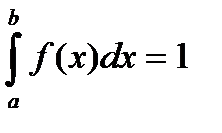                                                                                  (5.10)

 

Свойство (5.9, 5.10) называют условием нормировки. Общий вид функции плотности вероятности представлен на рис. 5.3.

3. Вероятность попадания непрерывной случайной величины в интервал 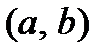 равна определенному интегралу от его плотности вероятности в пределах от а до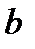

. 

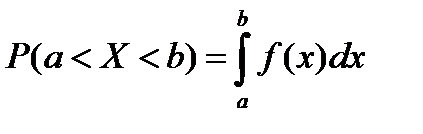Вероятность попадания в заданный промежуток [ а, b ], численно равна площади криволинейной трапеции с основанием [ а, b ].

 

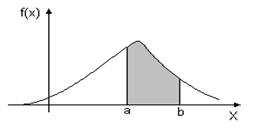
Рис.5.3. Определение вероятности попадания в заданный интервал

по функции плотности вероятности

 

Геометрически свойства плотности вероятности означают, что ее график лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

Пример. Случайная величина Х принимает значения  и имеет плотность . Найти число А, функцию распределения и .

Решение. 1) Для нахождения числа А воспользуемся свойствами плотности. Во-первых, 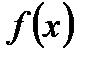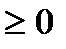. Это свойство будет выполнено при А > 0. Во-вторых, используем условие нормировки (5.10)

 

.

Поэтому случайная величина Х, заданная на промежутке 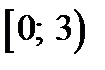 имеет плотность .

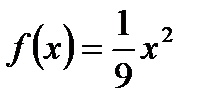2) Функцию распределения найдем интегрированием: .

3) Вероятность =

 

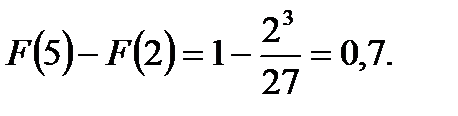
Числовые характеристики непрерывной случайной величины.  Понятия математического ожидания  и дисперсии , введенные для дискретной случайной величины можно распространить и на непрерывную случайную величину.

Для того чтобы найти математическое ожидание и дисперсию непрерывной случайной величины, следует закон ее распределения задать плотностью. Пусть случайная величина 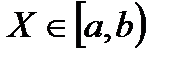 и имеет плотность 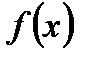. Тогда

Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси ОХ

 

.                                                                       (5.11)

 

Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат промежутку 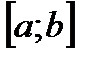определяется по формуле

 

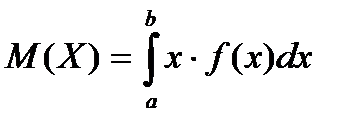.                                                                         (5.12)

 

Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси ОХ

 

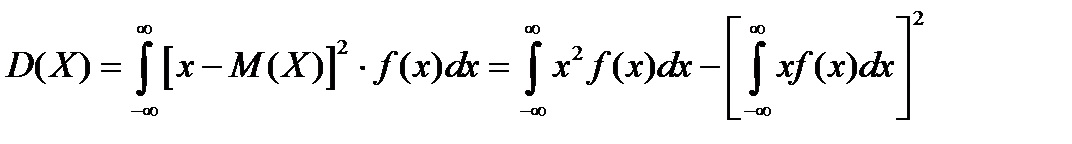                  (5.13)

или равносильным равенством

 

.

 

Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат промежутку 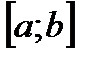определяется по формуле

 

.                       (5.14)

Среднеквадратическое отклонение  вычисляется как корень квадратный из дисперсии

 

.                                                                              (5.15)

Основные свойства математического ожидания и дисперсии для непрерывных случайных величин остаются такими же, как и для дискретных случайных величин.

 

Нормальный закон распределения непрерывной случайной величины.

Наиболее распространенным законом распределения для непрерывных случайных величин является нормальный закон распределения. Ему подчиняются практически все случайные величины, значения которых получаются непосредственным измерением или какими-нибудь линейными преобразованиями измеренных величин.

Определение. Случайная величина Х подчиняется нормальному закону распределения, если она определена на всей числовой оси и имеет плотность

 

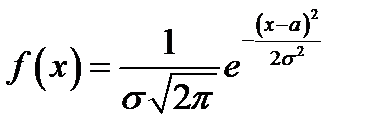.                                                                (5.16)

 

 Плотность определена на всей оси, ось абсцисс является асимптотой графика этой функции. Числовые характеристики нормального закона:

 

; .

 

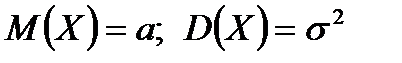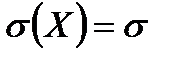График плотности называют нормальной кривой или кривой Гаусса.

Если 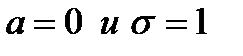, то нормальное распределение с такими параметрами называется стандартным или нормированным. Стандартное распределение табулируется, т. е. есть таблицы нормированного нормального закона. Плотность стандартной случайной величины имеет вид

.

 

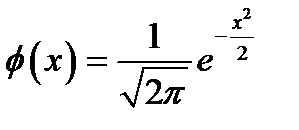 В общем случае график плотности имеет вид (рис. 5.4)

 

Рис. 5.4. График нормального закона распределения

 

Исследуем функцию 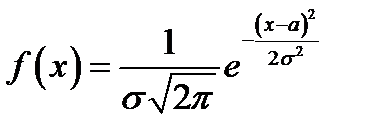 методами дифференциального исчисления:

1. Функция определена на всей числовой оси.

2. При всех значениях х функция принимает положительные значения, т.е. нормальная кривая расположена над осью 0 х.

3. Предел функции при неограниченном возрастании х (по абсолютной величине) равен нулю, т. е. ось ОХ – горизонтальная асимптота.

4. При 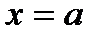 функция имеет максимум, равный .

5. Разность , содержащаяся в аналитическом выражении функции в квадрате, т. е. график функции симметричен относительно прямой .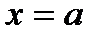

6. Точки 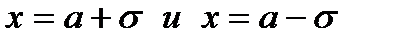  являются точками перегиба.

7. Изменение величины параметра а (математического ожидания) не изменяет формы кривой, а приводит лишь к ее сдвигу вдоль оси ОХ: вправо, если а возрастает и влево, если убывает.

8. Если меняется параметр  или 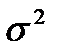, то меняется ордината максимума (рис. 5.5)

 

.

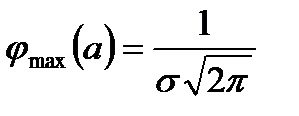Если  возрастает, то ордината максимума уменьшается, а так как площадь под кривой остается равной единице, то кривая делается более плоской. При уменьшении параметра  нормальная кривая вытягивается вверх, одновременно сжимаясь по бокам.

Рис. 5.5. Влияние величины дисперсии на форму кривой нормального закона

 

Следовательно, параметр а (математическое ожидание) характеризует положение центра, а параметр 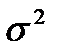(он же дисперсия) – форму нормальной кривой.

Заметим еще раз, что стандартным или нормированным называют нормальное  распределение, если М (Х) = a = 0, 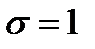. Плотность нормированного распределения

.

  

Функция распределения нормальной случайной величины не может быть найдена, так как интеграл 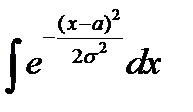 относится к классу неберущихся, он не выражается через элементарные функции. Однако аналогом функции распределения служит так называемая функция Лапласа (или интеграл вероятности):

.

 

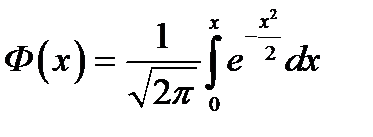Таблицы функции Лапласа есть практически в любом учебнике по теории вероятностей. Геометрически функция Лапласа представляет собой площадь под стандартной нормальной кривой на отрезке 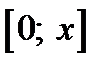 (рис. 12.6).

 

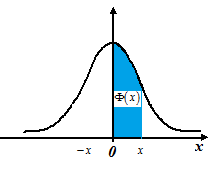
Рис. 5.6. Геометрический смысл функции Лапласа

 

Функция 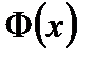 является нечетнойФ (-х) = - Ф (х), поэтому ее таблицы приведены только для , кроме того, Ф (х > 5)=0,5.

Функция общего нормального распределения:

 

 

 

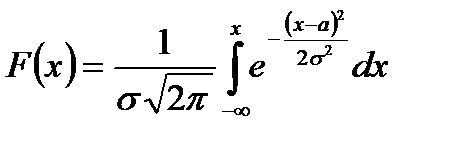
выражается через функцию Лапласа

 

.

 

Для нормированного распределения функция распределения выражается через функцию Лапласа. Функция Лапласа используется в ряде формул, связанных с нормальным законом распределения.

 

Вероятность попадания в заданный интервал нормальной случайной величины. Известно, что если случайная величина задана плотностью 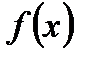, то вероятность того, что Х примет значение, принадлежащее интервалу 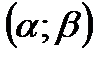, равна:

 

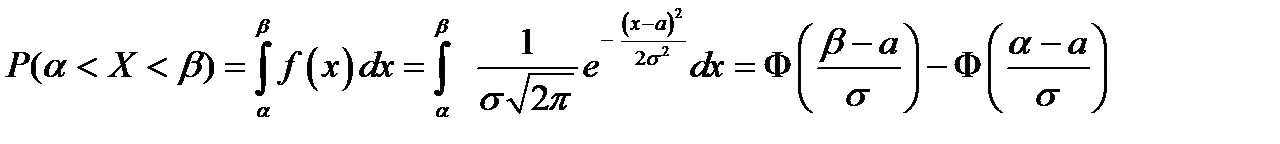.      (5.17)

 

Вычисление вероятности заданного отклонения. Часто требуется вычислить вероятность того, что отклонение нормально распределенной величины Х от своего математического ожидания по абсолютной величине меньше заданного положительного числа 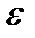, т. е. требуется найти вероятность осуществления неравенства .

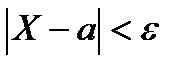Заменим это неравенство равносильным ему двойным неравенством 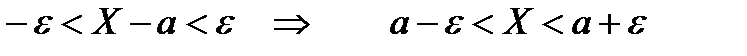. Пользуясь формулой (12.17), получим:

 

.

 

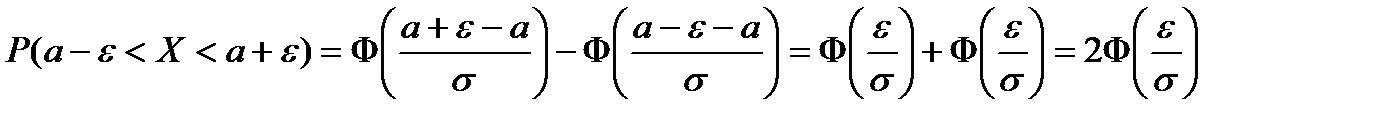Следовательно, вероятность отклонения 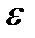 () нормальной величины от своего математического ожидания 

 

,                                                             (5.18)

в частности, при а = 0 справедливо равенство .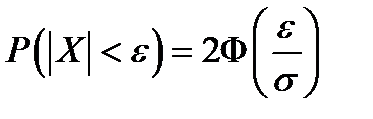

Пример 1. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 20 и 5. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (15, 25).

Решение.  Воспользуемся формулой:

 

 

 

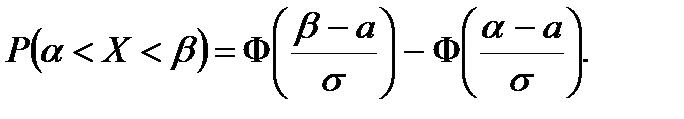
Подставив 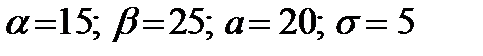, получим

.

Пример 2. Текущая цена ценной бумаги представляет собой нормально распределенную случайную величину Х со средним 100 усл. ед. и дисперсией 9. Найти вероятность того, что цена актива будет находиться в пределах от 91 до 109 у. е.

Решение.

.

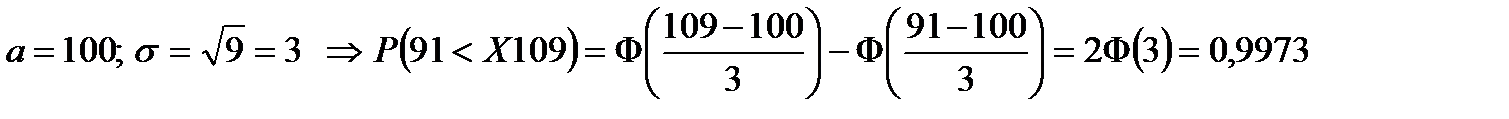Правило трех сигм. Если случайная величина Х имеет нормальное распределение с параметрами а и 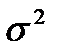, то практически достоверно, что ее значения заключены в интервале  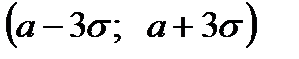 (рис. 5.7).

Рис. 5.7. Правило 3

 

По формуле (5.18) найдем вероятности отклонения :

Тем самым, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно составляет 1-0,9973=0,0027. Это означает, что такое может произойти только в 0,27% случаев, такие события считаются практически невозможными.

На практике правило «трех сигм» применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле выполняется, то есть основание считать, что изучаемая величина распределена нормально.

Пример. Имеется партия изделий, в которой могут быть бракованные изделия. Число бракованных изделий – нормально распределенная случайная величина, характеризующаяся так: среднее число бракованных изделий (математическое ожидание) составляет 12 %, а среднеквадратическое отклонение – 3 %. Отобрано 100 изделий. Какое число бракованных изделий окажется среди них?

Решение. Понятно, что ответить на вопрос точно в принципе нельзя. Однако, используя правило «трех сигм», легко найти ответ. Можно быть практически уверенным в том, что бракованных изделий будет не менее 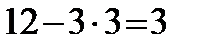 и не более 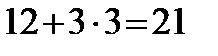. Формальная запись этого факта .