Пусть производится п независимых испытаний, в которых появление события А имеет вероятность р. Пусть число испытаний п достаточно велико 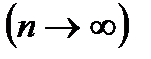 , а вероятность появления события А в каждом испытании мало
, а вероятность появления события А в каждом испытании мало 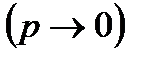 , при этом произведение пр сохраняет постоянное значение. Обозначим
, при этом произведение пр сохраняет постоянное значение. Обозначим 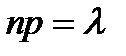 .
.
Дискретная случайная величина Х имеет закон распределения Пуассона с параметром 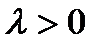 , если она принимает значения 0, 1, 2,…,
, если она принимает значения 0, 1, 2,…, 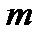 ,… (бесконечное, но счетное множество значений) с вероятностями
,… (бесконечное, но счетное множество значений) с вероятностями
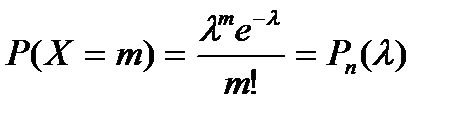 (4.10)
(4.10)
где т -число появлений события в п независимых испытаниях, 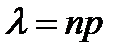 (среднее число появлений события в п испытаниях).
(среднее число появлений события в п испытаниях).
Ряд распределения закона Пуассона имеет вид:
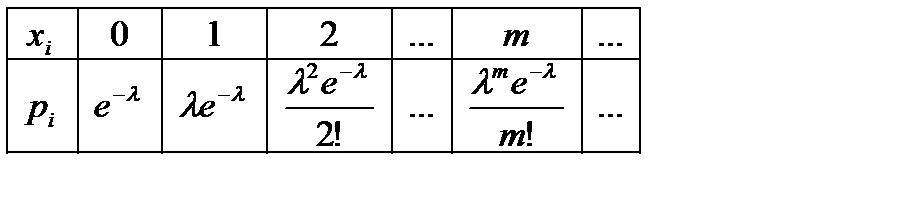
Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру этого закона, т. е.
 .
.
Замечание. При достаточно больших п (точнее, при 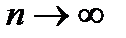 ) и малых значениях р (
) и малых значениях р (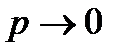 ) и при условии, что произведение
) и при условии, что произведение 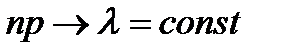 , закон распределения Пуассона является хорошим приближением биномиального закона. Так как при этом вероятность р события А в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
, закон распределения Пуассона является хорошим приближением биномиального закона. Так как при этом вероятность р события А в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
Пример. Для продвижения своей продукции на рынок фирма раскладывает по почтовым ящикам рекламные листки. Прежний опыт работы показывает, что примерно в одном случае из 2 000 следует заказ. Найти вероятность того, что при размещении 10 000 рекламных листков поступит хотя бы один заказ, среднее число поступивших заказов и дисперсию числа поступивших заказов.
Решение. Здесь 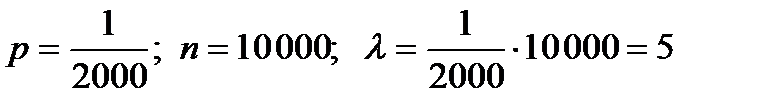 . Отсюда
. Отсюда
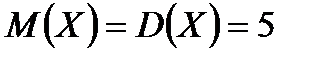 .
.
Вероятность того, что поступит хотя бы один заказ, найдем через вероятность противоположного события, т. е.
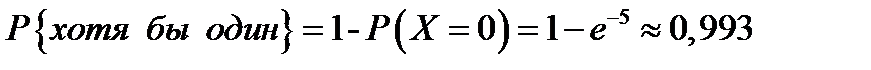 .
.
 2020-10-10
2020-10-10 816
816








