Оценки параметров генеральной совокупности по данным выборки

Определение неизвестных параметров выборки - следующая основная задача математической статистики. Решение этой задачи часто осуществляется при помощи метода моментов. Параметры выборки служат оценками параметров генеральной совокупности.

Генеральной средней называют среднее арифметическое значение признака у генеральной совокупности.

 

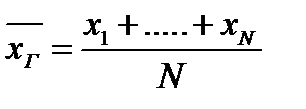,                                                                          (2.1)

 

где N – объем (количество данных) генеральной совокупности.

Оценкой генерального среднего служит выборочное среднее

 

,                                                                          (2.2)

где n – объем выборки. Если данные в выборке сгруппированы, то

 

,                                                             (2.3)

 

где x_i – варианты или середины соответствующих интервалов

Генеральная дисперсия есть среднее арифметическое квадратов отклонения значений от генеральной средней

 

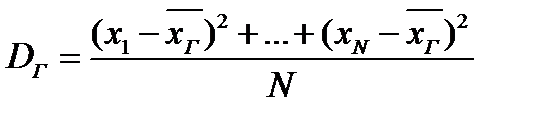.                                                             (2.4)

 

Ее оценкой является выборочная дисперсия

 

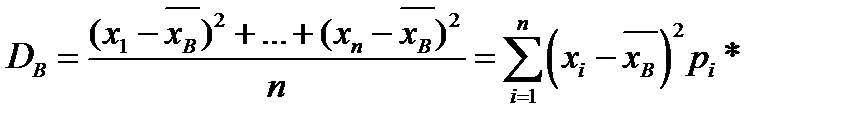,                                     (2.5)

или, для сгруппированных данных

 

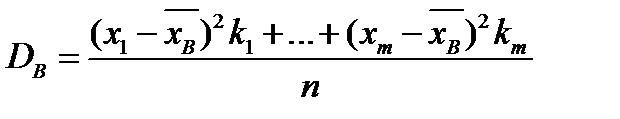   .                                                       (2.6)

 

Отсюда находится статистическое среднеквадратическое отклонение

 

.                                                                                      (2.7)

 

Ограниченное число опытов приводит к тому, что получаемые на их основе значения параметров генеральной совокупности содержат элемент случайности. Например, монета подбрасывалась пять раз и четыре раза выпадала цифра. Отсюда можно сделать вывод о том, что среднее число выпадений цифры в одном опыте равно 0.8. В то же время, очевидное значение этой характеристики - 0.5 (если монета и техника подбрасывания "правильные"). Однако к такому выводу приходят при очень большом количестве подбрасывании монеты. Так, Ж. Бюффон подбрасывал монету 4048 раз, и цифра выпадала в 1956 случаев, т. е. среднее число появлений цифры при одном подбрасывании было получено равным 0.48.

Случайное значение искомого параметра, вычисленного на основании данного статистического материала, называют оценкой параметра.

Пусть проведено n опытов и получены значения случайной величины (x ₁, x ₂,..., x_n). Требуется построить оценку (называемой иногда точечной оценкой) неизвестного параметра "g", которую будем обозначать g^~. Эта оценка есть функция опытных величин, т. е.

 

g^~ = g^~(x ₁, x ₂,..., x_n).

 

Задача состоит в том, чтобы построить наиболее подходящие оценки. Здесь под термином наиболее подходяще подразумевается предъявление следующих требований:

 

1. Оценка параметра должна быть состоятельной. Это означает, что при увеличении числа опытов, оценка все более приближается (стремится по вероятности) к точному значению параметра

 

g^~ ® g при n ® ¥.

 

1. Оценка параметра должна быть несмещенной, т.е. ее математическое ожидание должно равняться оцениваемому параметру

 

M[g^~] = g.

 

Несмещенность означает отсутствие постоянной ошибки оценки в какую-то одну сторону.

3. Желательно, чтобы оценка параметра была эффективной, т. е. оценка по сравнению с другими должна обладать наименьшей дисперсией.

 

Сформулированным требованиям отвечает выборочное среднее.

Выборочная дисперсия является смещенным параметром, поэтому вводят так называемую исправленную дисперсию и при n > 30 считается, что разница между исправленной и выборочной дисперсией несущественна.

                                                                                                       

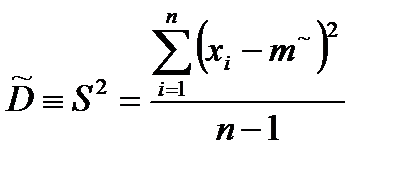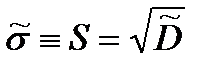,   .                                                   (2.8)

 

Качество статистического оценивания. Пусть по результатам опыта построена точечная оценка g^~ некоторого параметра g. Необходимо проверить  насколько эта оценка точна и достоверна.

Точность оценивания характеризуется абсолютной ошибкой, которая возникает, если параметр заменить его точечной оценкой, т. е.

 

Dg = ½g - g’½.

 

Однако определить истинную погрешность Dg невозможно, поскольку g^’ - случайная величина, а сам параметр g неизвестен.

В математической статистике задачу оценки точности решают следующим образом.

Откладывают от g’ вправо и влево такую величину e_b > 0, что неслучайное (хотя и неизвестное) значение g, как показано на рис.2.1, оцениваемого параметра практически наверняка оказывается в пределах случайного интервала I_b = (g’ - e_b, и g’ + e_b).

Введем понятие доверительной вероятности и доверительного интервала. Вероятность b называется доверительной, если интересующее нас событие A, происходящее с этой вероятностью, считается практически гарантированным (достоверным). Как правило, b близка к единице и выбирается равной 0.9, 0,95, 0,99 или 0,999. Максимальной вероятной погрешностью статистической оценки называется ее максимально возможное отклонение e_b  > 0 от оцениваемого параметра, гарантируемое с вероятностью b.

 

 

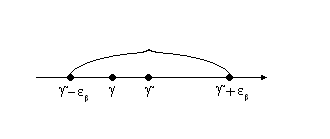
Рис. 2.1.. Доверительный интервал

Пусть задана доверительная вероятность (надежность) b. Тогда условие

P(½g’ - g½ < e_b) = b,                                                                   (2.9)

определяет доверительный интервал I_b  = (g’ - e_b, g’ + e_b), который с вероятность b накрывает неизвестный параметр g. Можно сказать, что доверительный интервал - интервал значений параметра g, совместимых (в вероятностном смысле) с опытными данными.

Очевидно, что выражение (1.9) по заданному b позволяет найти e_b и, наоборот, по заданной величине e_b можно найти b. Доверительный интервал определяет точность найденной оценки параметра, а доверительная вероятность ее достоверность.

Изложим методы нахождения доверительных интервалов для математического ожидания 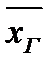 = m (g º m), если известно, что случайная величина имеет нормальный закон распределения.

Малая выборка

На практике малой считается выборка с объемом меньше 30. Пусть по формулам (2.2) или (2.3) найдена оценка математического ожидания, а по формуле (2.8) оценка дисперсии. Тогда для определения доверительного интервала используют распределение Стьюдента, функция распределения которого S (t,n), в отличии от нормального закона, зависит только от размера выборки n. По распределению Стьюдента значение 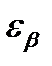 есть

 

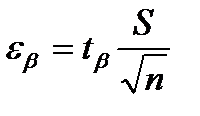,                                                                                        (2.10)                                                            

где 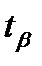 значение аргумента функции S (t,n) при данном n, для которого выполняется равенство S (t,n) = β.

Приведем таблицу значений 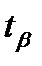 при разных объемах выборок n для доверительных вероятностей β = 0,95; 0,99; 0,999 (табл. 3).

Таким образом, чтобы найти доверительный интервал для оценки математического ожидания по заданной доверительной вероятности, необходимо:

1. По (2.2) вычислить оценку математического ожидания 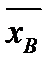, по (2.8) вычислить оценку дисперсии S², а по ней величину S. 

Т а б л и ц а 3.

n			5	6	7	8	9	10	11	12	13
β	0.95		2.78	2.57	2.45	2.37	2.31	2.26	2.23	2.20	2.18
	0.99		4.60	4.03	3.71	3.50	3.36	3.25	3.17	3.11	3.06
	0.999		8.61	6.86	5.96	5.41	5.04	4.78	4.59	4.44	4.32
n			14	15	16	17	18	19	20	25	30
β		0.95	2.16	2.15	2.13	2.12	2.11	2.10	2.09	2.06	2.05
		0.99	3.01	2.98	2.95	2.92	2.90	2.88	2.86	2.80	2.76
		0.999	4.22	4.14	4.07	4.02	3.97	3.92	3.88	3.75	2.66

2. Для величины b по таблице значений функции распределения Стьюдента определить t_b.

3. Вычислив по (2.10) e_b, записать доверительный интервал

I_b = ( - e_b, + e_b).

Большая выборка, т. е. объем выборки больше 30. Согласно закону больших чисел она приближенно распределена по нормальному закону. Запишем условие (2.9), выразив правую часть через функцию Лапласа

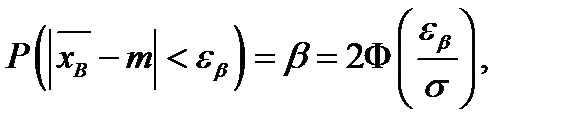                                                                 (2.11)                       

где среднеквадратическое отклонение можно приближенно положить равным величине 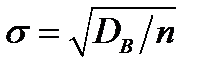. Зная доверительную вероятность β, найдем по таблице значений функции Лапласа величину 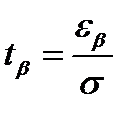. Отсюда .

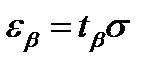Таким образом, чтобы найти доверительный интервал для оценки математического ожидания по заданной доверительной вероятности, необходимо:

1. по (2.5) вычислить оценку дисперсии, а по ней величину ;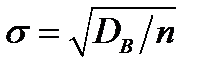

2. для величины b/2 по таблице приведенной функции распределения Лапласа определить t_{b =} ;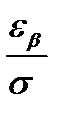 

3. вычислив e_b по 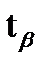,  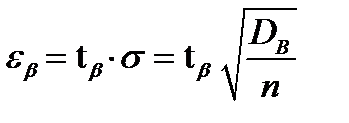 , можно записать доверительный интервал

I_b = ( - e_b, + e_b).

Приведем сокращенную таблицу значений b и t_b (таб. 4).

Пример. Случайная величина имеет нормальный закон распределения со средним квадратичным отклонением s = 1. Известна выборочная средняя 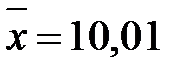 и объем выборки n =10. Найти доверительный интервал для оценки неизвестного математического ожидания а с заданной надежностью β=0,85.

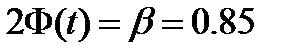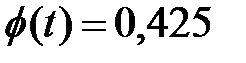Решение. Зная  т.е. , где 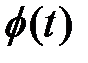 - табулированная функция Лапласа найдем  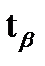= 1,44. Так как σ нам дано D = σ², то e_b =  Следовательно, доверительный интервал 9,55 < а < 10,47.

                                                                             

Т а б л и ц а 4.

b	0.80	0.82	0.84	0.86	0.88	0.90
tb	1.282	1.340	1.404	1.475	1.554	1.643
b	0.92	0.94	0.95	0.96	0.98	0.99
tb	1.750	1.880	1.960	2.053	2.325	2.576

 

Заключение

 

Изучение математики в высшем учебном заведении преследует разные цели. Это и тренировка логического мышления, и возможность решать математическими методами всевозможные прикладные задачи и изучение универсального символьного языка, который используется в естественно-научных, технических и гуманитарных дисциплинах.