Раздел: Дифференциальное исчисление
Тема: Производная функции
I. Определение производной
Определение 1. Пусть функция y=f(x) определена в некоторой окрестности точки х0. Для любой точки этой окрестности приращение аргумента Δх определяется формулой Δx = х - х0.
| 0 |
| y |
| x |
| y=f(x) |
| f(x0+Δx) |
| f(x0) |
| x0 |
| x0+Δx |
| Δx |
| Δy |
| Приращение функции |
| Приращение аргумента |
Рис. 1.1. Определение производной функции
Определение 3. Производной функции y = f(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
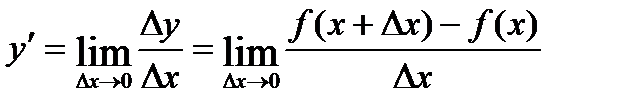 (1.1)
(1.1)
Производная функции имеет несколько обозначений: y', f '(x), 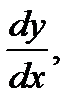
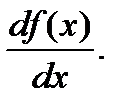 Иногда в обозначении производной используется индекс, указывающий, по какой переменной взята производная, например, y'x.
Иногда в обозначении производной используется индекс, указывающий, по какой переменной взята производная, например, y'x.
Определение 4. Нахождение производной функции называется дифференцированием этой функции.
Определение 5. Если функция в точке х имеет конечную производную, то функцию называют дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка Х, называется дифференцируемой на этом промежутке.
II. Схема вычисления производной
Производная функции y = f(x) может быть найдена по следующей схеме:
1. Дадим аргументу х приращение Δх ≠ 0 и найдем наращенное значение функции у+Δу = f(х+Δх ).
2. Находим приращение функции Δу = f(x+Δx) - f(x).
3. Составляем отношение 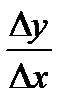 .
.
4. Находим предел этого отношения при Δх→0, т.е. 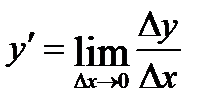 (если этот предел существует).
(если этот предел существует).
Пример 1. Найти производную функции y = f(x) = x2-2x+2.
Решение.
1. Даем аргументу х приращение Δх≠0.
2. Находим наращенное значение функции у+Δу=f(x+Δx)=(x+Δx)2-2(x+Δx)+3=x2+2x Δx+(Δx)2-2x-2Δx+3.
3. Находим приращение функции Δу = f(x+Δx) - f(x) = x2 +2xΔx +(Δx)2- 2x -2Δx+3 - x2 +2x - 3 = 2xΔx + (Δx)2 - 2Δx.
4. Составляем отношение 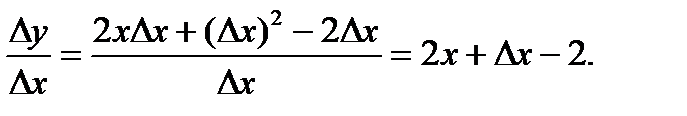
5. Находим предел 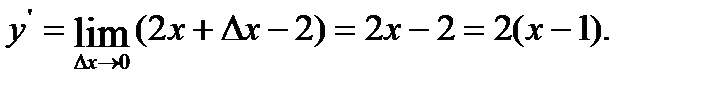
III. Производные основных элементарных функций
| Название функции | Функция | Производная функции |
| “C” – число (постоянная величина) | y= f(х)=С (С=const) | 0 |
| Степенная фунция | 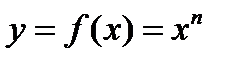 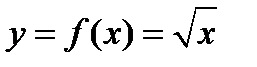
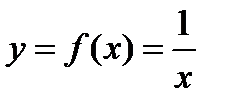
| 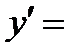 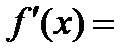 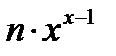
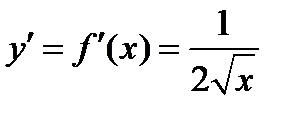
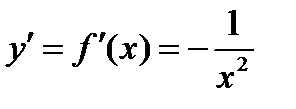
|
| Экспоненциальная функция (е» 2,7 - экспонента) | y = f(х)= eх | 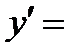 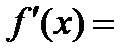 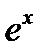
|
| Показательная функция (а – постоянное число) | y = f(х)=aх | 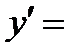 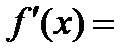 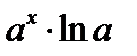
|
Логарифмическая функция
(натуральный логарифм)
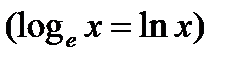
| y= f(х) =ln х | 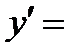 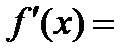 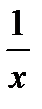
|
| Тригонометрическая функция | y= f(х)=sin x | 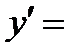 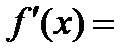 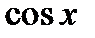
|
| Тригонометрическая функция | y= f(х)=cos x | 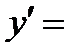 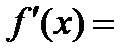 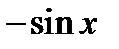
|
| Тригонометрическая функция | y = f(х) = tg x | 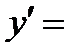 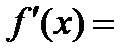 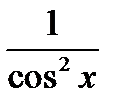
|
| Тригонометрическая функция | y = f(х) = ctg x | 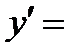 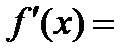 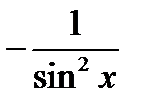
|
| Тригонометрическая функция | y = f(х) = arcsin x | 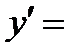 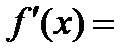 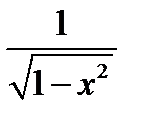
|
| Тригонометрическая функция | y = f(х) = arccos x | 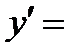 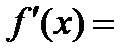 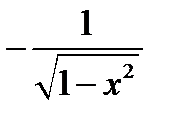
|
| Тригонометрическая функция | y = f(х) = arctg x | 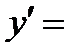 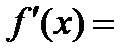 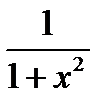
|
| Тригонометрическая функция | y = f(х) = arcctg x | 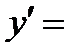 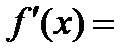 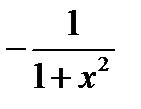
|
 2020-10-10
2020-10-10 390
390







