Вращательным движением абсолютно твердого тела называется движение, при котором все его материальные точки описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.
Основное уравнение динамики для твердого тела, вращающегося вокруг неподвижной оси, имеет вид:
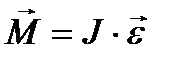 , (1.41)
, (1.41)
где М – момент силы, действующей на тело; e – угловое ускорение;
J –момент инерции тела относительно оси вращения.
Из формулы (1.10) следует, что угловое ускорение сообщаемое телу вращающим моментом зависит от момента инерции тела: чем больше момент инерции, тем меньше угловое ускорение, и наоборот. Мгновенное угловое ускорение равно первой производной по времени от угловой скорости:
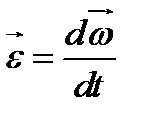
Линейное и угловое ускорения связаны соотношением: a = e×R,
где R – радиус окружности.
Момент инерции является основной физической величиной, характеризующей инертные свойства твердого тела при вращательном движении, подобно тому, как масса характеризует инертные свойства тела при поступательном движении. Момент инерции материальной точки относительно оси равен произведению массы m точки на квадрат расстояния r от точки до оси вращения:
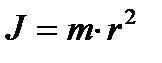 (1.42)
(1.42)
Момент инерции измеряется в кг·м2.
Момент инерции твердого тела равен сумме моментов инерции материальных точек, из которых состоит это тело:
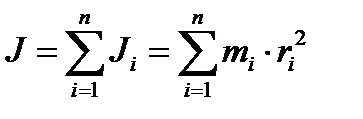 (1.43)
(1.43)
В отличие от массы, момент инерции данного тела может иметь бесконечное множество значений в соответствии с множеством осей вращения.
Если плотность тела во всем объеме постоянна, т.е. тело однородно, и если тело имеет правильную геометрическую форму, то вычисление моментов инерции относительно главных осей (проходящих через центр масс) можно осуществить при помощи интегрирования.
Приведем формулы для расчета момента инерции однородных тел геометрически правильной формы относительно оси симметрии.
1. Момент инерции тонкого стержня длиной l:
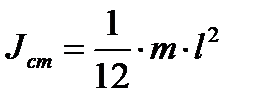
2. Момент инерции диска:
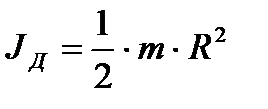
3. Момент инерции шара:
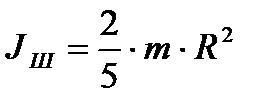
4. Момент инерции толстостенного кольца радиусами R1 и R2:

5. Момент инерции тонкостенного кольца (обруча):
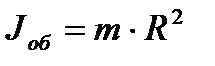
Если известен момент инерции тела относительно главной оси, то можно определить момент инерции относительно любой другой оси, параллельной данной, по теореме Штейнера:
J = JC+ ma2, (1.44)
где JC – момент инерции относительно оси ОО, проходящей через центр масс С; m – масса всего тела.
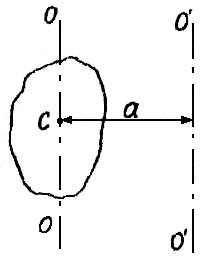
Рисунок 1.11 – Иллюстрация теоремы Штейнера
O'О' – произвольная ось, относительно которой вычисляется момент инерции; a – расстояние между осями ОО и O'О'.
Моментом силы относительно неподвижной оси называется произведение силы F на плечо ℓ:
M = F · ℓ (1.45)
Плечом ℓ силы называется кратчайшее расстояние от оси до линии действия силы. Момент силы измеряется в Н·м.
Момент импульса относительно неподвижной оси вращения каждой точки тела равен:
L i = m i× v i× r i, (1.46)
где ri – радиус окружности, описываемой каждой точкой тела; vi – ее линейная скорость
v i = ω·ri,
где ω – угловая скорость вращения тела.
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:
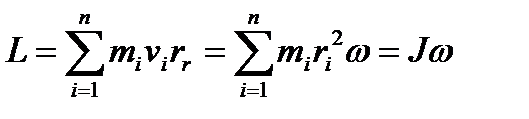 (1.47)
(1.47)
Основное уравнение динамики вращательного движения с учетом
(1.47) можно записать в виде:
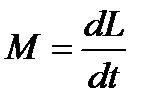 (1.48)
(1.48)
Экспериментальный способ определения моментов инерции тел основан на наблюдении крутильных колебаний исследуемого тела.
Уравнение вращательного движения тела вокруг оси, проходящей через точку подвеса, имеет вид:
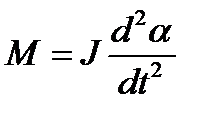 , (1.49)
, (1.49)
где α – угол поворота тела вокруг вертикальной оси; М – момент упругой силы относительно той же оси, действующей со стороны закрученного на угол α торсиона; J – момент инерции тела.
При малых деформациях этот момент пропорционален деформации:
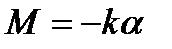 , (1.50)
, (1.50)
где k – коэффициент жесткости при кручении.
Уравнение (1.49) с учетом (1.50) примет вид:
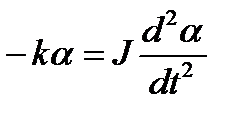 (1.51)
(1.51)
или 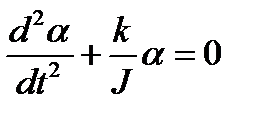 (1.52)
(1.52)
В общем виде уравнение (1.52) можно записать:

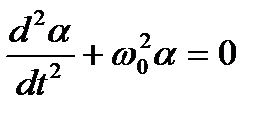 (1.53)
(1.53)
где 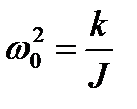 – собственная круговая частота гармонических колебаний. Решением уравнения (1.53) является функция, описывающая незатухающие гармонические колебания:
– собственная круговая частота гармонических колебаний. Решением уравнения (1.53) является функция, описывающая незатухающие гармонические колебания:
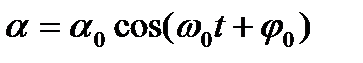 , (1.54)
, (1.54)
где α – угол поворота тела в момент времени t; α0 – амплитуда колебаний;  – фаза колебаний; φ0 – начальная фаза.
– фаза колебаний; φ0 – начальная фаза.
Период колебаний тела определяется как:
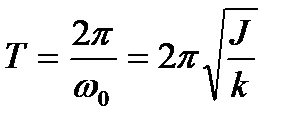 (1.55)
(1.55)
 2020-10-10
2020-10-10 180
180








