2020-10-10
118
Разность между средними двух выборок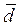 
):
= 
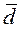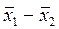
Разность между средними двух генеральных совокупностей (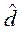
):
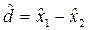
Допустимое расхождение между 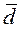и 
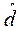представляет собой неточность в определении разности между двумя генеральными совокупностями (Δ), которой можно пренебречь.
Ошибка разности (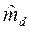
) представляет собой квадратный корень из суммы квадратов ошибок средних двух сравниваемых генеральных совокупностей:
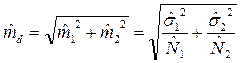
Допустимая неточность (Δ) – произведение стандартного значения критерия Стьюдента при заданном числе степеней свободы (df) и уровне значимости на ошибку разности ():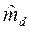
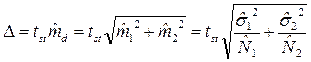
Это означает, что при достаточной численности выборок N 1 и N 2 выборочная разность не будет отличаться от генеральной разности между 
и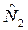 
более чем на величину 
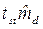или менее чем на заданную неточность Δ.
Для вычисления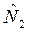 
приравняем его к выражению a 
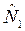где а – коэффициент пропорциональности между 
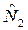и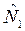 
, равный 
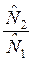. Тогда:
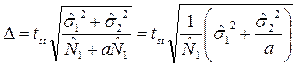
Решим это уравнение относительно 
:
Пять величин (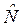
, 
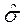, Δ, k, tst), которые необходимы для планирования достаточной численности выборок при изучении достоверности различий между ними, определяются по тем же правилам, что и при изучении средних.
Пример 2. Планируется определить достаточные объемы выборок для сравнения двух летних сортов груши («Чижовская» и «Лада») по массе плода (г) в условиях Центрального региона РФ. Таким образом, необходимо запланировать допустимые численности взвешиваемых плодов (шт.) у двух сортов груши (N 1 и N 2) для достоверной оценки разности между генеральными средними. Масса плода по сравнению с длиной листа менее вариабельна. Однако, и в этом случае, для минимизации случайной вариации плоды отбирают в фазу полной потребительской спелости (конец августа), среднего размера, с нескольких деревьев, достигших возраста хозяйственного плодоношения.
Зададим необходимые для вычислений параметры. Наметим приблизительные объёмы генеральных совокупностей (численности плодов 
) сравниваемых сортов. Пусть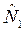 
≈500 шт., 
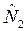≈600 шт. тогда:
a =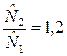 
Зададим величины генеральных средних квадратических отклонений признака «масса плода, г» у сравниваемых сортов (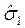
и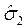 
). Для этого приблизительно определим минимальную и максимальную массу плода у сорта Чижовская: 
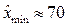г, 
г для оценки размаха изменчивости. Используем правило 6 сигм. Тогда:
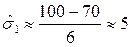г
Аналогично зададим минимальную и максимальную массу плода у сорта Лада: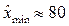 
г, 
г.,тогда:
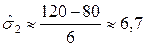г
Предварительно наметим допустимую неточность ∆≈5 г. Примем t -критерий равный: t 05=1,96. При заданных параметрах численность взвешиваемых плодов у сорта Чижовская (N 1) должна быть не менее 10 шт., а у сорта Лада (N 2) – 12 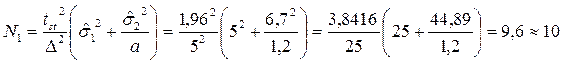шт.:
шт.
N 2= aN 1=1,2 N 1=12 шт.
Практическое задание 3.2. Необходимо определить достаточные объемы выборок для сравнения двух сортов сливы домашней («Тульская черная» и «Евразия 21») по массе плода (г) в условиях Центрального региона РФ.
Решение:
