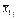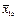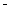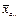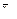2020-10-10
1514
Структура двухфакторного дисперсионного комплекса. В табл. 10.1. представлена структура двухфакторного дисперсионного комплекса в общем виде. Градации фактора А обычно располагают по строчкам, фактора В – по столбцам таблицы.
Таблица 10.1. Структура двухфакторного дисперсионного комплекса
| Градации фактора А | Градации фактора В | Σ х i.. | ni .. |
| |||||||||||||
| 1 | j | b | |||||||||||||||
| 1 | х 111 | Σ x 11. | n 11. |
| … | х 1j1 | Σ x 1j. | n 1j. |
| … | х 1b1 | Σ x 1b. | n 1b. |
| Σ х i.. | ni .. |
|
| х 112 | х 1j2 | х 1b2 | |||||||||||||||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| i | х i11 | Σ x i1. | n i1. |
| … | х ij1 | Σ x ij. | n ij. |
| … | х ib1 | Σ x ib. | n ib. |
| Σ х i.. | ni .. |
|
| x i12 | x ij2 | x ib2 | |||||||||||||||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| a | x a11 | Σ x a1. | n a1. |
| … | x aj1 | Σ x aj. | n aj. |
| … | x ab1 | Σ x ab. | n ab. |
| Σ х i.. | ni .. |
|
| x a12 | x aj2 | x ab2 | |||||||||||||||
| Σ x .j. | Σ x .1. | … | Σ x .j. | … | Σ x .b. | Σ х i.. | ni .. |
| |||||||||
| n .j. | n .1. | … | n .j. | … | n .b. | ||||||||||||
 |
| … |
| … |
| ||||||||||||
Параметры, входящие в двухфакторный дисперсионный комплекс:
хijk отдельное наблюдение (варианта);
Σ x … сумма всех наблюдений по комплексу;
Σ xi .. суммы наблюдений по градациям фактора А;
Σ x . j . суммы наблюдений по градациям фактора В;
Σ xij . суммы наблюдений по сочетаниям градаций фактора А и В;
N число всех наблюдений по комплексу (объем комплекса);
ni .. число наблюдений по градациям фактора А;
n . j . число наблюдений по градациям фактора В;
nij . число наблюдений по сочетаниям градаций фактора А и В;
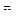общее среднее арифметическое по комплексу;
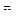средние арифметические по градациям фактора А;
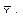средние арифметические по градациям фактора В;
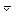средние арифметические по сочетаниям градаций фактора А и В.
a число градаций по фактору А
b число градаций по фактору В
Если число наблюдений по сочетаниям градаций фактора А и В (nij .) константно, то комплекс является равномерным. В случае если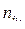 
варьирует - комплекс будет неравномерным.
Типы варьирования переменных в двухфакторном дисперсионном комплексе. В анализируемом комплексе различают 5 типов варьирования переменных:
1) общая вариация – варьирование отдельных наблюдений (хijk) вокруг средней по комплексу ();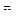
2) вариация, связанная с влиянием фактора А – варьирование средних по градациям фактора А (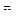) вокруг средней по комплексу ();
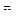3) вариация, связанная с влиянием фактора В – варьирование средних по градациям фактора В (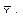) вокруг средней по комплексу ();
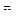4) вариация, связанная со взаимодействием факторов А и В – варьирование средних по сочетанию градаций факторов А и В (
) вокруг средней по комплексу (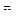) без учета вариации, связанной с влиянием факторов А и В;
5) случайная вариация отдельных наблюдений (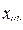
) вокруг средних по сочетанию градаций факторов А и В ().
Суммы квадратов отклонений вариант от средней (SS). Поскольку типов вариации переменных в двухфакторном комплексе пять, вычисляются 5 различных SS:
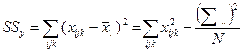
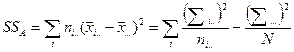
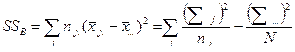
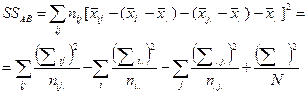
Приведенные формулы используются неравномерного комплекса. Если комплекс равномерный, соответствующие численности (ni .., n.j., nij.) выносятся за знак суммы в виде знаменателя дроби (в числителе – единица) и вычисления значительно упрощаются.
Если суммы отклонений рассчитаны правильно должно выполняться следующее равенство:
Числа степеней свободы (df). Для каждой суммы квадратов отклонений рассчитывается своё число степеней свободы:
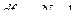
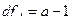
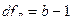
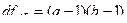
где 
- среднее число наблюдений по сочетаниям градаций факторов А и В.
Если числа степеней свободы рассчитаны правильно, должно выполняться равенство:
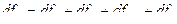
Средние квадраты (ms). Необходимо вычислить 4 средних квадрата:
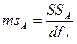
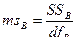
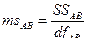
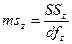
Критерии Фишера (F). Вычисляются 3 эмпирических значения критерия Фишера:
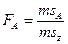
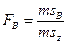
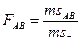
Для каждого эмпирического значения по таблицам определяются стандартные критерия Фишера на 5% и 1% уровнях значимости (приложения 2.4 и 2.5). Если какое-либо эмпирическое значение F > F 05 и F > F 01, нулевая гипотеза об отсутствии влияния данного фактора (факторов) или взаимодействия факторов отклоняется.
Если F 05 < F < F 01, то на 5% уровне значимости нулевую гипотезу следует отклонить, а на 5% - принять. В этом случае рекомендуется продолжить экспериментальные исследования по изучению влияния данного фактора на изменчивость переменного.
Если F < F 05, то нулевая гипотеза об отсутствии влияния соответствующего фактора принимается.
Структура средних квадратов и вычисление дисперсий. Если влияние фактора или взаимодействия факторов недостоверно соответствующие дисперсии приравниваются к 0. Если доказано достоверное влияние фактора, то необходимо вычислить величину соответствующей дисперсии. В большинстве экспериментов оба фактора имеют фиксированные градации. Рассмотрим структуру средних квадратов и оцениваемые параметры для этой модели дисперсионного анализа (табл. 10.3):
Таблица 10.3. Структура средних квадратов и формулы для вычисления дисперсий в двухфакторном дисперсионном анализе с фиксированными градациями факторов
| Структуры средних квадратов | Формулы для вычисления дисперсий |
 |  |
 |  |
 |  |
 |  |
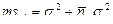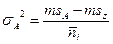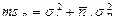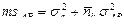После вычисления дисперсий у достоверно влияющих факторов, их взаимодействия и случайной вариации вычисляется общая дисперсия:
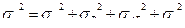
Дисперсии необходимы для вычислений долей влияния источников вариации переменного.
Определение доли влияния факторов. Доли влияния источников вариации вычисляют как частные от деления соответствующей дисперсии на общую дисперсию. Обычно доли выражают в процентах:
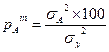
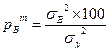
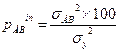
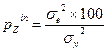
Вычисление наименьшей существенной разности (НСР). НСР вычисляется для каждого среднего по градациям факторов и их сочетанию. При проведении двухфакторного анализа максимально вычисляется 3 типа НСР. Если источник вариации недостоверно влияет на переменное, то НСР для сравнения соответствующих средних не вычисляется. Для вычисления НСР необходимо установить ошибки средних по следующим формулам:
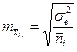(ошибка средних по градациям фактора А)
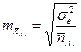(ошибка средних по градациям фактора В)
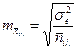(ошибка средних по сочетанию градаций факторов А и В)
Стандартное значение критерия Тьюки (Q 05). Определяется по таблице (приложение 2.6), по тем же правилам, которые обсуждались в предыдущем разделе. НСР вычисляют путем перемножения соответствующей ошибки на коэффициент Тьюки (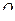
05).
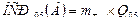
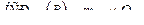
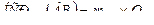
Оценка достоверности различий между средними. Для проведения оценки строятся матрицы разностей между средними, и затем эти разности сравнивают с соответствующими НСР05. Если разность превышает величину НСР05, она считается достоверной.
Число матриц разностей средних может равняться трем, если оба фактора и их взаимодействие достоверно влияют на признак: 1) матрица разностей между средними по градациям фактора А; 2) матрица разностей между средними по градациям фактора В; 3) матрица разностей между средними по сочетанию градаций факторов А и В.
Итоговая результативная таблица. Сведение результатов двухфакторного дисперсионного анализа в итоговую таблицу (табл. 10.4.)
Таблица 10.4. Результаты двухфакторного дисперсионного анализа данных об изменчивости...
| Источник вариации | SS | df | ms | σ2 | Fэмп | F05 | F01 | pin% | НСР05 |
| Общая | SSy | dfy | - | σy 2 | - | - | - | py in% | - |
| Фактор А | SSA | dfA | msA | σA 2 | FA | F 05(A) | F 01(A) | pA in% | НСР A |
| Фактор В | SSB | dfB | msB | σB 2 | FB | F 05(B) | F 01(B) | pB in% | НСР B |
| Взаимодействие АВ | SSAB | dfAB | msAB | σAB 2 | FAB | F 05(AB) | F 01(AB) | pAB in% | НСР AB |
| Случайные отклонения | SSz | dfz | msz | σe 2 | - | - | - | pe in% | - |
Выводы. Выводы должны содержать информацию по: 1) оценке достоверности влияния факторов и их взаимодействия; 2) долям влияния факторов, их взаимодействия и случайной вариации; 3) результатам оценки достоверности различий между средними по градациям достоверно влияющих факторов и их взаимодействия.
Пример 1. Изучали длину междоузлий (мм) в средней части однолетнего побега у деревьев 4-х сортов абрикоса на 3-х клоновых подвоях:
| Сорт абрикоса | Клоновый подвой | ||
| ВВА-1 | Дружба | ВСГ | |
| Краснощекий | 62; 68; 64; 65;60 | 55; 42;51 | 53; 55; 50; 53 |
| Никитский | 55; 52; 49; 48 | 58; 65; 62; 64; 62 | 57; 59; 47; 53 |
| Арзами | 37; 36;42 | 56; 70; 67 | 40; 46;51; 55; 56 |
| Венгерский | 59; 58; 54 | 60; 53; 56 | 45; 57; 52 |
Какое влияние на длину междоузлий оказывают генотипические различия между сортами абрикоса, клоновые подвои и их взаимодействие?
Решение:
1. Копируем содержание таблицы в Excel
2. Строим дисперсионный комплекс
3. Определим основные параметры, суммы и компоненты формул:
объем комплекса (N) = 45
число градаций по фактору А (а) = 4
число градаций по фактору В (b) = 3
среднее число наблюдений по градациям фактора А (ni..)=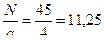 
среднее число наблюдений по градациям фактора В (n.j.) =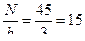 
среднее число наблюдений по сочетанию градаций АВ (nij.) = 
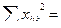137193
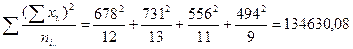
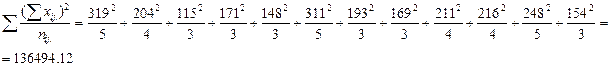
4. Вычислим суммы квадратов отклонений наблюдений от средних (SS):
=
= 
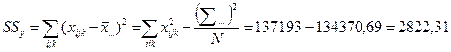
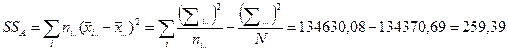
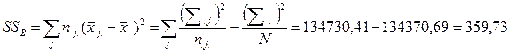
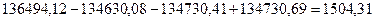
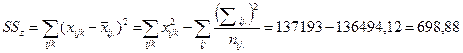
Проверим корректность вычислений:
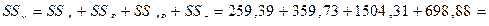2822,31
5. Вычислим числа степеней свободы (df):
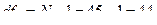
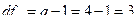
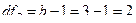
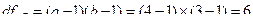
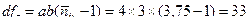
Проверим корректность вычислений:
6. Вычислим средние квадраты (ms):
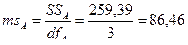
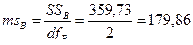
Двухфакторный дисперсионный комплекс анализа изменчивости длины междоузлий однолетнего побега абрикоса (мм) в зависимости от сорта (фактор А) и клонового подвоя (фактор В)
| Фактор А (сорт абрикоса) | Фактор В (клоновый подвой) | Σi.. | ni.. | xi.. | |||||||||||||||||||||||
| ВВА-1 | Дружба | ВСГ | |||||||||||||||||||||||||
| длина междолузлий, мм | Σij. | nij. | xij. | длина междолузлий, мм | Σij. | nij. | xij. | длина междолузлий, мм | Σij. | nij. | xij. | ||||||||||||||||
| Краснощекий | 62 | 68 | 64 | 65 | 60 | 319 | 5 | 63,8 | 55 | 42 | 51 |
|
| 148 | 3 | 49,3 | 53 | 55 | 50 | 53 |
| 211 | 4 | 52,8 | 678 | 12 | 56,5 |
| Никитский | 55 | 52 | 49 | 48 |
| 204 | 4 | 51,0 | 58 | 65 | 62 | 64 | 62 | 311 | 5 | 62,2 | 57 | 59 | 47 | 53 |
| 216 | 4 | 54,0 | 731 | 13 | 56,2 |
| Арзами | 37 | 36 | 42 |
|
| 115 | 3 | 38,3 | 56 | 70 | 67 |
|
| 193 | 3 | 64,3 | 40 | 46 | 51 | 55 | 56 | 248 | 5 | 49,6 | 556 | 11 | 50,5 |
| Венгерский крупный | 59 | 58 | 54 |
|
| 171 | 3 | 57,0 | 60 | 53 | 56 |
|
| 169 | 3 | 56,3 | 45 | 57 | 52 |
|
| 154 | 3 | 51,3 | 494 | 9 | 54,9 |
| Σ.j. | 809 | 821 | 829 | 2459 | 45 | 54,6 | |||||||||||||||||||||
| n.j. | 15 | 14 | 16 | ||||||||||||||||||||||||
| x.j. | 53,9 | 58,6 | 51,8 | ||||||||||||||||||||||||
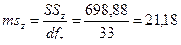
7. Вычислим критерии Фишера (F):
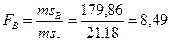
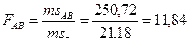
8. Определим стандартные значения критерия Фишера для каждого фактора и их взаимодействия по таблицам (стат. табл. IV-V):
для фактора А: F05 (dfa=3; dfz=33)= 2,90; F01(dfа=3; dfz=33)= 4,48;
для фактора В: F05 (dfb=2; dfz=33)= 3,29; F01(dfb=2; dfz=33)= 5,33;
для взаимодействия АВ: (dfаb=6; dfz=33)= 2,39; F01(dfab=6; dfz=33)= 3,40;
9. Сравним эмпирические значения критерия Фишера со стандартными:
FA=4,08>F05=2,90; FA=4,08<F01=4,48;
FB=8,49>F05=3,29; FB=8,49>F01=5,33;
FAB=11,84>F05=2,39; FAB=11,84>F01=3,40;
10. Сформулируем статистические выводы:
по фактору А:нулевая гипотеза отклоняется на 5% уровне значимости и принимается на 1% уровне значимости;
по фактору В: нулевая гипотеза отклоняется на 1% уровне значимости;
по взаимодействию факторов АВ: нулевая гипотеза отклоняется на 1% уровне значимости.
11. Вычислим дисперсии (σ2) для тех факторов, которые достоверно влияют:
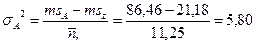
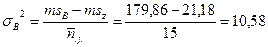
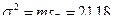
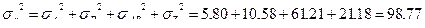
12. Вычислим доли влияния факторов (pin%):
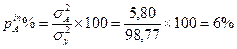
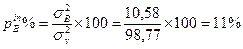
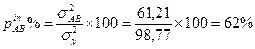
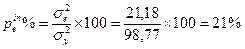
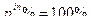
13. Вычислим ошибки групповых средних по факторам и взаимодействию (mx), ошибки вычисляются только для тех средних, по которым доказано достоверное влияние фактора:
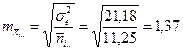
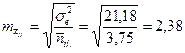
14. Определяем критерий Тьюки (Q05) по стат. табл.VI:
для фактора А: Q05(а=4; dfZ=33)=3,8
для фактора В: Q05(b=3; dfZ=33)=3,5
для взаимодействия АВ: Q05(аb=12; dfZ=33)=5,0
15. Вычисляем НСР05:
для фактора А: НСР05=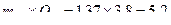 
для фактора В: НСР05=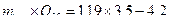 
для взаимодействия АВ: НСР05=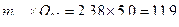 
16. Сводим все данные в результативную таблицу:
Результаты двухфакторного дисперсионного анализа данных об изменчивости длины междоузлий (мм) на однолетних побегах абрикоса в зависимости от генотипа сорта (фактор А) и клонового подвоя (фактор В):
| Источник вариации | SS | df | ms | σ2 | F | F05 | F01 | pin% | НСР05 |
| Общая | 2822,31 | 44 |
| 98,77 |
|
|
| 100 |
|
| Фактор А (сорт) | 259,39 | 3 | 86,46 | 5,80 | 4,08 | 2,90 | 4,48 | 6 | 5,2 |
| Фактор В (подвой) | 359,73 | 2 | 179,86 | 10,58 | 8,49 | 3,29 | 5,33 | 11 | 4,2 |
| Взаимодействие АВ | 1504,31 | 6 | 250,72 | 61,21 | 11,84 | 2,39 | 3,40 | 62 | 11,9 |
| Случайная | 698,88 | 33 | 21,18 | 21,18 |
|
|
| 21 |
|
17.Гистограммы групповых стредних:
Рис. 11.1. Групповые средние по градациям фактора А
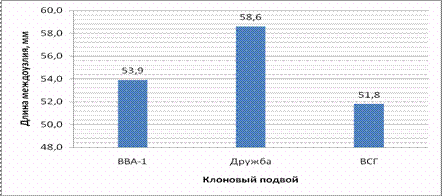
Рис. 11.2. Групповые средние по градациям фактора В
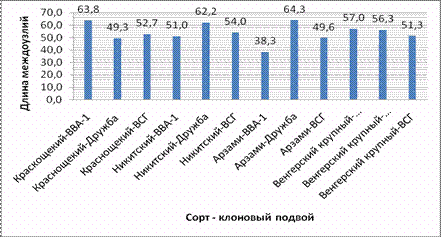
Рис. 11.3. Групповые средние по градациям взаимодействия факторов АВ
18. Круговая диаграмма долей влияния факторов:
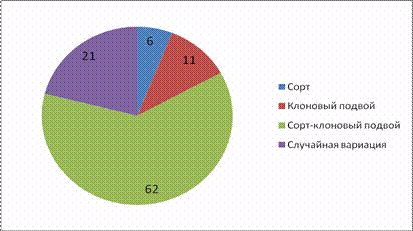
Рис.11.4. Доли влияния факторов
19. Проведем сравнение групповых средних между собой:
Матрица разностей групповых средних по фактору А
|
| xi.. | ||||
| 56,5 | 56,2 | 50,5 | 54,9 | ||
| xi.. | 56,5 | 0,3 | 6,0 | 1,6 | |
| 56,2 | 5,7 | 1,3 | |||
| 50,5 | -4,4 | ||||
| 54,9 | |||||
| НСР05=5,2 | |||||
Матрица разностей групповых средних по фактору В
|
| x.j. | |||
| 53,9 | 58,6 | 51,8 | ||
| x.j. | 53,9 | -4,7 | 2,1 | |
| 58,6 | 6,8 | |||
| 51,8 | ||||
| НСР05=4,2 | ||||
Матрица разностей групповых средних по взаимодействию АВ
|
| х ij. | ||||||||||||
| К-ВВА | К-Д | К-ВСГ | Н-ВВА | Н-Д | Н-ВСГ | А-ВВА | А-Д | А-ВСГ | ВК-ВВА | ВК-Д | ВК-ВСГ | ||
| х ij. | 63,8 | 49,3 | 52,7 | 51,0 | 62,2 | 54,0 | 38,3 | 64,3 | 49,6 | 57,0 | 56,3 | 51,3 | |
| К-ВВА | 63,8 | 14,5 | 11,1 | 12,8 | 1,6 | 9,8 | 25,5 | -0,5 | 14,2 | 6,8 | 7,5 | 12,5 | |
| К-Д | 49,3 | -3,4 | -1,7 | -12,9 | -4,7 | 11.0 | -15,0 | -0,3 | -7,7 | -7,0 | -2,0 | ||
| К-ВСГ | 52,7 | 1,7 | -9,5 | -1,3 | 14,4 | -11,6 | 3,1 | -4,3 | -3,6 | 1,4 | |||
| Н-ВВА | 51,0 | -11,2 | -3,0 | 12,7 | -13,3 | 1,4 | -6,0 | -5,3 | -0,3 | ||||
| Н-Д | 62,2 | 8,2 | 23,9 | -2,1 | 12,6 | 5,2 | 5,9 | 10,9 | |||||
| Н-ВСГ | 54,0 | 15,7 | -10,3 | 4,4 | -3,0 | -2,3 | 2,7 | ||||||
| А-ВВА | 38,3 | -26,0 | -11,3 | -18,7 | -18,0 | -13,0 | |||||||
| А-Д | 64,3 | 14,7 | 7,3 | 8,0 | 13,0 | ||||||||
| А-ВСГ | 49,6 | -7,4 | -6,7 | -1,7 | |||||||||
| ВК-ВВА | 57,0 | 0,7 | 5,7 | ||||||||||
| ВК-Д | 56,3 | 5,0 | |||||||||||
| ВК-ВСГ | 51,3 | ||||||||||||
| НСР05=11,9 | |||||||||||||
20. Общие выводы по дисперсионному анализу:
1. Установлено достоверное влияние генотипа сорта привоя, клонового подвоя и их взаимодействия на изменчивость длины междозлий у однолетних побегов абрикоса. Однако, влияние клонового подвоя и взаимодействия «сорт-подвой» достоверно на 1% уровне значимости, но генотипа сорта – на 5% уровне значимости. Поэтому для уточнения достоверности влияния сорта привоя на длину междоузлий исследования следует продолжить.
2. Наиболее сильное влияние на длину междоузлий оказывает взаимодействие «сорт-подвой» (доля влияния 62%). Это означает, что сорта привои по разному реагируют на клоновые подвои. Вторым фактором по силе влияния является подвой (доля влияния составляет 11%). Наименее всего влияет сорт привой (доля влияния составляет 6%). Доля случайной вариации составляет 21%.
3. Наименьшей длиной междоузлий в среднем на всех подвоях характеризуется сорт Арзами (50,5 мм), наибольшей – сорт Краснощекий (56,5 мм). Сорт Арзами достоверно отличается по длине междоузлий от сортов Краснощекий и Никитский.
4. Наименьшей длиной междоузлий в среднем по всем привоям характеризуется подвой ВСГ (51,8 мм), наибольшей – подвой Дружба (58,6 мм). Подвой Дружба достоверно отличается по дине междоузлий от подвоев ВВА-1 и ВСГ.
5. Среди сорто-подвойных комбинаций следует отметить сочетание Арзами – ВВА-1, где наблюдается минимальная длина междозлий (38,3 мм). Максимальную длину междоузлий наблюдали у сорта Арзами на подвое Дружба (64,3 мм).
Практическое задание 10.1. Черенки туи западной обрабатывали препаратом «2У». Определите влияние типа раствора (спиртовой, органический №1, органический №2) и концентрации препарата (2 мл/л, 5 мл/л, 10 мл/л) на суммарную длину корней (см):
| Тип раствора | Концентрация | Суммарная длина корней, см | |||||||||
| спирт. раствор | 2 мл/л | 18 | 72 | 56 | 68 | 32 | 46 | ||||
| 5 мл/л | 42 | 14 | 48 | 8 | 12 | 48 | 6 | 46 | 48 | 24 | |
| 10 мл/л | 36 | 48 | 38 | 54 | 32 | 78 | 48 | 84 | |||
| орг. раствор 1 | 2 мл/л | 102 | 86 | 98 | 64 | 62 | 32 | 64 | 64 | ||
| 5 мл/л | 18 | 56 | 46 | 16 | 28 | 46 | 56 | 38 | 28 | ||
| 10 мл/л | 53 | 32 | 18 | 46 | 14 | 96 | 24 | 18 | 26 | 84 | |
| орг. раствор 2 | 2 мл/л | 64 | 12 | 8 | 14 | 46 | 48 | 54 | 62 | 52 | |
| 5 мл/л | 22 | 64 | 42 | 36 | 28 | 24 | 68 | 26 | 18 | 18 | |
| 10 мл/л | 52 | 45 | 58 | 24 | 24 | 46 | 52 | ||||
Решение:
