Механической обработки

В разделе 6.3 рассмотрены первичные погрешности механиче­ской обработки резанием и даны необходимые расчеты для опре­деления числовых значений этих погрешностей. Однако главным является вопрос о нахождении суммарной погрешности обработки.

Для определения ожидаемой точности необходимо суммировать первичные погрешности. Задачу о суммировании решают особо для каждого случая обработки и в зависимости от того, какую сущ­ность в данном процессе имеет каждая погрешность. На ожидае­мую точность влияют многие факторы, однако суммирование в большинстве случаев можно проводить по первичным погрешно­стям, рассмотренным выше.

Рассмотрим вопрос суммирования при обработке заготовок на настроенных станках с использованием приспособлений. Предпо­ложим, что имеется такой случай обработки, когда каждая из пер­вичных погрешностей представляет собой звено размерной цепи. Тогда ожидаемую точность Д можно представить как замыкающее звено цепи и суммирование первичных погрешностей производить алгебраически:

                                                 (6.2)

Задачу следует решать методом «максимума-минимума». При этом все первичные погрешности здесь отнесены к направлению выдерживаемого размера. Значение 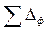 необходимо определять с учетом взаимной компенсации погрешностей технологической системы. При обработке тел вращения  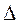для диаметральных раз­меров нужно определять без учета 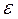, равно как и для случая двух­сторонней обработки элементов изделия набором режущих ин­струментов.

Расчет значения 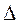 по формуле (6.2) является достаточно прос­тым. Вместе с тем точность расчета оказывается низкой, а резуль­тат почти всегда завышенным.

Возможен и другой метод расчета. Каждую первичную погреш­ность можно представить как вектор, модуль которого характери­зует поле рассеивания погрешности или (что менее точно) разность предельных значений погрешности. Тогда значение 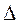 следует опре­делять в векторной форме:

                                                     (6.3)

Этот метод лишь в исключительных случаях можно применять на практике, поскольку необходимо знать направление, в котором проявляется данная погрешность, что связано с трудностями в практической работе технолога.

Каждый из предложенных выше методов суммирования имеет существенные недостатки, которые могут быть в значительной

степени ослаблены, если первичные погрешности рассматривать как случайные величины. Такой подход вполне соответствует сути расчетно-статистического метода определения точности.

Первые пять слагаемых в формуле (6.2) — случайные величины. Поэтому суммировать их необходимо по закону квадратного корня:

                                              (6.4)

где р — коэффициент, определяющий процент риска получения брака при обработке; 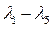— коэффициенты, характеризующие законы распределения каждой из первичных погрешностей.

Риск возникает в связи с тем, что нельзя утверждать с полной определенностью, что рассеяние данной первичной погрешности соответствует данному закону распределения. При р = 1 вероят­ность брака составляет 32%, при р = 2 она снижается до 4,5%, а при р = 3 доходит до 0,27%.

Коэффициенты 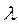 имеют вполне определенные значения для каждого закона распределения. Так, для закона нормального рас­пределения 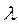=1/9, для распределения Симпсона 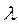= 1/6, для за­кона равной вероятности, а также для случаев, когда о законе рас­пределения данной первичной погрешности ничего не известно (либо мало известно), — 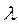= 1/3.

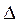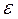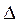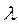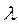Из практики известно, что y,  и _н имеют распределение, близкое к нормальному, поэтому 1= ₂ = 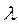₃ = 1/9. Распределение 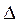_и близко к закону равной вероятности, следовательно, 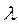₄ = 1/3. Характер распределения 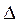T мало изучен, поэтому 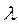₅ = 1/3. При р = 3 формула 6.4 имеет вид:

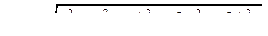                                                               (6.5)

Величина 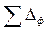 не является случайной, поэтому ее нельзя сум­мировать под знаком корня, с учетом этой погрешности ожидаемая погрешность:

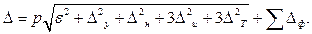                                                     (6.6)

Последней формулой можно широко пользоваться на практике. Значения первичных погрешностей, суммируемых под знаком кор­ня, представляют собой поле рассеяния этих величин.

При обработке одной или нескольких заготовок используют метод пробных ходов и промеров. В этом случае ожидаемую по­грешность рассчитывают по формуле:

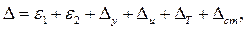                                                                         (6.7)

где 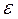1 — погрешность установки режущего инструмента; 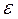₂ — погрешность формы обработанной поверхности или погрешность ее положения относительно измерительной базы; 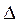у — погрешность формы обрабатываемой поверхности из-за копирования первич­ных погрешностей заготовки; 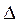_и — погрешность формы поверхно­сти в результате износа режущего инструмента; 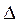_т — погрешность формы одной детали из-за тепловых деформаций системы; 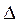_ст — погрешность формы обрабатываемой поверхности, вызываемая геометрическими погрешностями станка.