2020-10-09
122
Пусть задано множество 
упорядоченных пар чисел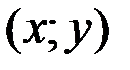 
.
Функцией двух переменных называется закон (соответствие)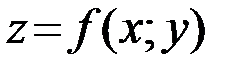 
, по которому каждой паре чисел 
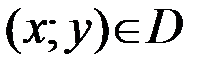сопоставляет единственное число 
. При этом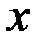 
и 
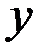называются независимыми переменными, а 
– зависимой переменной или функцией. Множество называется областью определения функции, множество значений, принимаемых в области определения функции, называется множеством значений функции (обозначается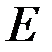 
).
Функция двух переменных, как и функция одной переменной может задаваться аналитически, в виде таблицы или в виде графика. График функции двух переменных представляет собой некоторую поверхность в трехмерном пространстве. Каждой точке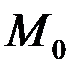 
с абсциссой 
и ординатой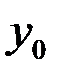 
в плоскости 
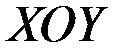соответствует точка 
, где 
– аппликата.
Определение 4.1. Число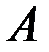 
называется пределом функции двух переменных 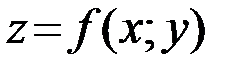то есть при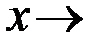 
, 
(или, что то же самое, при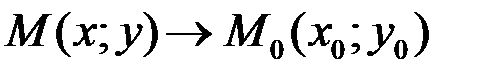 
), если для любого сколь угодно малого числа 
найдется такое число 
, всех что для всех 
и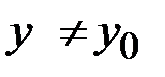 
и удовлетворяющих неравенству 
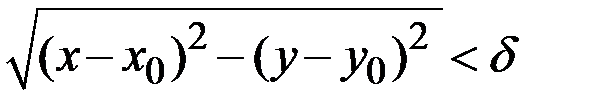выполняется неравенство 
.
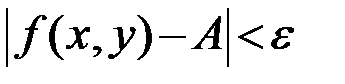Записывают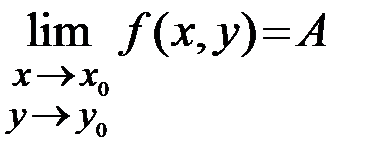 
или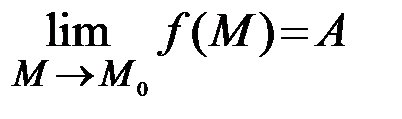 
.
Непрерывность функции двух переменных.
Функция 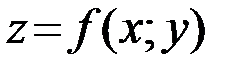(или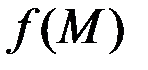 
) называется непрерывной в точке 
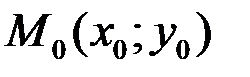, если она:
а) определена в этой точке и некоторой ее окрестности,
б) имеет предел 
,
в) этот предел равен значению функции в этой точке, то есть 
.
Функция 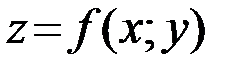, непрерывная в каждой точке некоторой области называется непрерывной в этой области. Точки, в которых нарушается хотя- бы одно из условий непрерывности функцииназываются точками разрыва этой функции.
