2020-10-09
240
График дифференцируемой функции 
называется выпуклым (выпуклым вверх) на интервале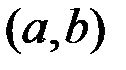 
, если он расположен ниже любой ее касательной на этом интервале (рис 3.7).
График дифференцируемой функции называется вогнутым (выпуклым вниз) на интервале 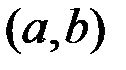, если он расположен выше любой ее касательной на этом интервале (рис 3.7).
Рис 3.7
Точка графика непрерывной функции , отделяющая область выпуклости от области вогнутости (и наоборот) называется точкой перегиба (рис 3.7).
Интервалы выпуклости и вогнутости находят с помощью следующей теоремы.
Теорема 3.10. Если функция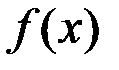 
во всех точках интервала 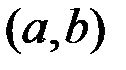имеет отрицательную вторую производную, то есть 
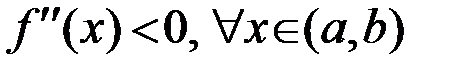, то ее график – выпуклый (выпуклый вверх) на интервале .
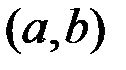Если функция 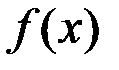во всех точках интервала 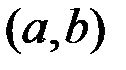имеет положительную вторую производную, то есть 
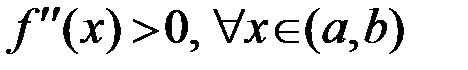, то ее график – вогнутый (выпуклый вниз) на интервале .
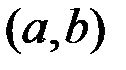Очевидно, перегиб может возникать лишь в точках, где вторая производная равна нулю или не существует. Эти точки еще называют подозрительными на перегиб.
|
|
|
Точки перегиба находят с помощью следующей теоремы.
Теорема 3.11. (Достаточные условия существования точек перегиба)
Пусть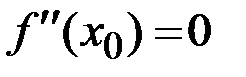 
или не существует 
, то есть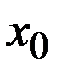 
– точка подозрительная на перегиб.
Если вторая производная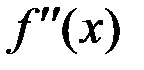 
меняет знак, при переходе через точку 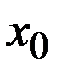, то точка графика с абсциссой 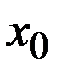– точка перегиба.
