Полный дифференциал функции двух переменных

Пустьфункция 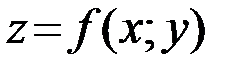определена в некоторой окрестности точки 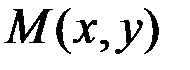. Полное приращение функции в точке  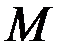(приращение по переменным  и ) определяется и обозначается .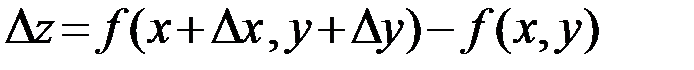

Функция 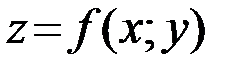называется дифференцируемой в точке 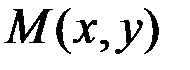, если ее полное приращение в этой точке можно представить в виде

,

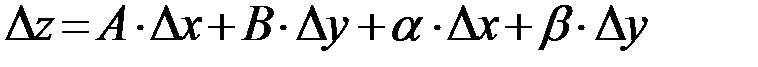где 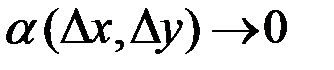, при   и .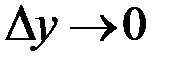

 Выражение 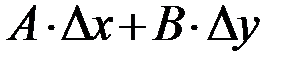 представляет собой полный дифференциал 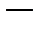главную часть приращения функции, его обозначают . Выражения   и 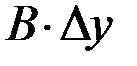 называются собой частнымидифференциалами. Для независимых переменных  и 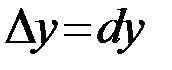, поэтому выражение для полного дифференциала  принимает вид .

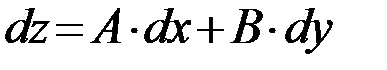Теорема 4.2.(необходимое условие дифференцируемости функции).

Если функция 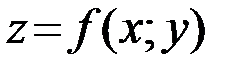  дифференцируема в точке 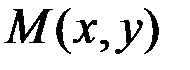, то она непрерывна в этой точке, имеет в ней частные производные  и ,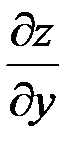

причем 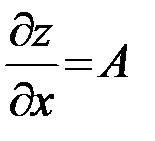 и .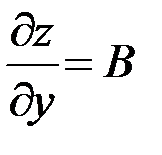

Следствие 4 .1.   Формула полного дифференциала имеет вид .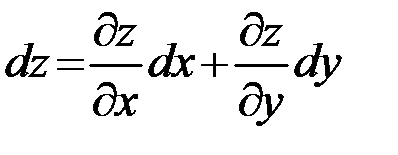

Теорема 4.3. (достаточное условие дифференцируемости функции).

Если функция 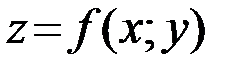  имеет частные производные  и 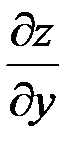 в точке 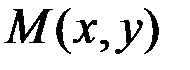, то она дифференцируема в этой  точке и ее полный дифференциал вычисляется по формуле .

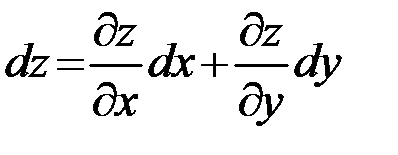Экстремум функции двух переменных.

Понятия максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной переменной.

Пусть функция 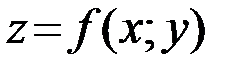определена в некоторой области 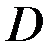. Точка  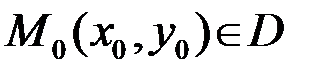называется точкой максимума функции 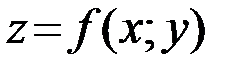, еслидля любых  точек  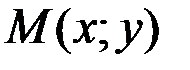из -окрестности (достаточно малой окрестности) точки 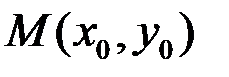 выполняется неравенство 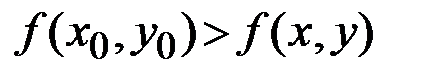(см. Рис 4.1).

 

Аналогично определяется точка минимумафункции 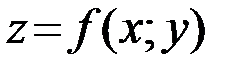,: для любых  точек  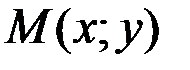из -окрестности (достаточно малой окрестности) точки 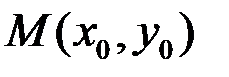 выполняется неравенство 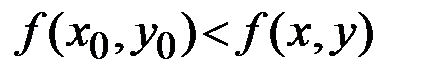(см. Рис 4.1).

Значение функции в точке максимума (минимума) называется максимумомфункции (минимумом функци) (см. Рис 4.1). 

 

 

Рис 4.1

 

 

Необходимые и достаточные условия экстремума функции двух переменных.