Теорема 4.4. (необходимые условия экстремума)

Если в точке 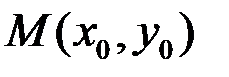  дифференцируемая  функция  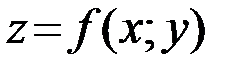 имеет экстремум, то ее частные производные равны нулю в этой точке: , .

Точка 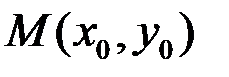, в которой частные производные равны нулю называется стационарной точкой функции .

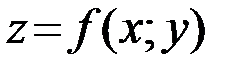Стационарные точки и точки, в которых не существует хотя бы одна частная производная, называются критическимиточками функции .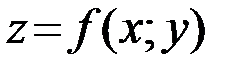

Теорема 4.5. (достаточное условие экстремума).

Пусть в стационарной точке 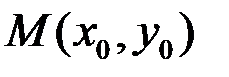 и в некоторой ее окрестности функция  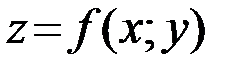имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке  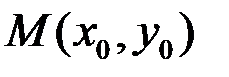 значения , , . Обозначим .

Тогда:

1. если , то функция 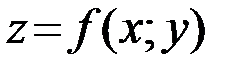 в точке  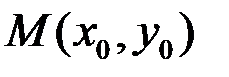имеет экстремум: максимум, если , минимум, если ;

2. если , то функция 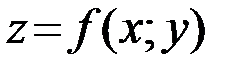 не имеет экстремума;

3. если , то экстремум может быть, а может не быть  необходимо дополнительное исследование.

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ