Определив расчетные усилия, переходим к нахождению требуемой наименьшей высоты балки. Из условия, что нормы жесткости:
 =
= 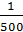
Основное допускаемое напряжение для стали Ст3 [σ]p = 1400 кг/см2, т.к. от суммарного момента М1=45.0(Т*м), напряжение достигает заданного значения [σ]pто от момента вызванного сосредоточенного момента М1=36,0Т*м. Напряжение будет составлять
[σ]p * 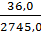 = 0,8 [σ]p
= 0,8 [σ]p
Эту величину и следует учитывать вместо: [σ]p = 1400 кг/см2 при определении требуемой высоты балки.
Прогиб балки отдвух сосредоточенных сил расположенных симметрично в пролете равен:
f=  )2]
)2]
E – модуль упругости: 2*106 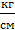 , для Ст 3
, для Ст 3
𝒥 - коэффициент устойчивости
Если P*a выразить через М, то:
f = 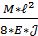 [1 -
[1 -  (
( )2]
)2]
Выполнив ряд преобразований получим следующую формулу:
f = 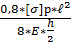 [1 -
[1 -  (
( )2]
)2]
Учитывая условия жесткости  =
= 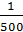 из формулы выразим h – высоту балки:
из формулы выразим h – высоту балки:
h= 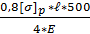 [ 1-
[ 1-  (
( )2]
)2]
h =  [ 1-
[ 1-  (
( )2] =
)2] = 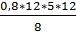 =68.25см
=68.25см
h = 68.25 см,
E=2*106
a= 
| d=3 |
| a |
| 6M |
| 12M |
Рисунок 8–Расстояние от опоры до первого груза
Чтобы определить требуемую высоту балки из условия ее наименьшего сечения. Нужно задаться толщиной вертикального листа. Для этого используем приближенные соотношения:
Sв - толщинавертикального листа.
Sв= 
Sв= 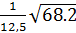 = 0.66 см =≈7 мм
= 0.66 см =≈7 мм
Sв=7мм
Требуемую высоту определяем из условия наименьшего веса.
h = 1,3 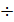 1,4
1,4 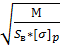
h = 1,3  = 1,3
= 1,3  = 1,3 * 67,763 = 88,0919
= 1,3 * 67,763 = 88,0919  88,09 см
88,09 см
Так как наименьшая требуемая высота 68,2 см меньше, чем высота найденная из условия наименьшего веса 88,09 то при подборе сечения будем принимать в расчет высоту 68,9 см
Принимаем общую высоту балки: 68 см
Высоту вертикального листа вычисляем из соотношения:
hв = (0,95 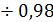 ) * h = 0,98* 68= 66,64 см
) * h = 0,98* 68= 66,64 см
Принимаем hв = 66 см
 2020-10-11
2020-10-11 211
211








