2020-10-11
155
Требуемый момент инерции и момент поперечного сечения балки двутаврового профиля вычисляем по формуле:
𝓨тр = Wтр 
𝓨тр= 3214* 
= 109276см4
Момент инерции подобранного вертикального листа размером 660х7 определяем по формуле:
𝓨в = 
4
Из соотношения 𝓨тр = 
в + 2𝓨г находим момент инерции для двух горизонтальных листов:
𝓨тр = в + 2𝓨г
2𝓨г= 𝓨тр- 
в
2𝓨г=109276-16770,6=92505,4см4
С другой стороны величина момента инерции записывается в следующем виде:
𝓨г = 2 [𝓨0 + Fг(
2 ]
“𝓨0” это момент инерции горизонтального листа относительно собственной оси. Эта величина крайне мола, поэтому в расчетах ей пренебрегают.
г = 2[Fг (
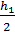)2]
h1– это расстояние между центрами тяжести горизонтальных листов.
L AQItABQABgAIAAAAIQBPygNL4gAAAAsBAAAPAAAAAAAAAAAAAAAAAM0JAABkcnMvZG93bnJldi54 bWxQSwUGAAAAAAQABADzAAAA3AoAAAAA ">
| h1=67 |
| 68 |
| 66 |
| 7 |
Рисунок 9 – Расстояние между центрами тяжести горизонтальных листов
Fг – площадь горизонтального листа:
Fг = 
= 
= 41.21см2
Fг =41см2
Учитываем, что толщина полок всегда должна быть больше чем стенки, принимаем сечение горизонтального листа 410 х 10 мм
Для подобранного поперечного сечения балки определим уточненное значение момента инерции
𝓨ут= 
+2[ 
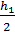г * Sг ( )2]
𝓨ут= 
𝓨ут = 108801,93 см4
