2020-10-11
98
Рассматривается статически неопределимая рама (рис. 18).
  |
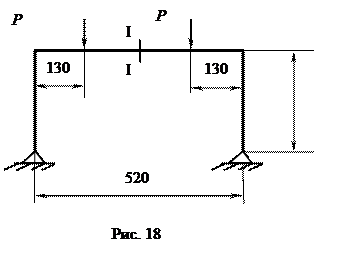Задача 1 раз статически неопределима (четыре неизвестных реакции в шарнирно неподвижных опорах, можно составить три независимых уравнения равновесия). Решаем задачу методом сил. Каноническое уравнение имеет вид:
.
  |
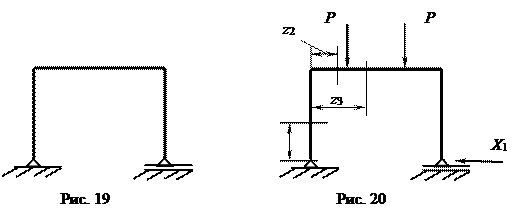Выбираем основную систему (рис. 19). Эквивалентную систему получаем, приложив взамен отброшенной связи неизвестную силу X 1 (рис. 20).
Прикладываем к основной системе поочередно внешние нагрузки и единичную силу взамен отброшенной реакции опоры (рис. 21 и 22).
Находим реакции (показаны на рис. 21 и 22), составляем выражения изгибающих моментов для каждого из нагружений:
   |
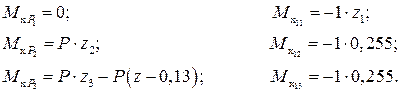
Учитывая симметрию рамы, рассматриваем три участка, удваивая все вычисленные значения коэффициентов канонических уравнений. Коэффициенты 
и 
определяем с помощью интеграла Мора:
Тогда
Определим реакции с учетом найденного значения неизвестной силы X 1 (рис. 23) и построим эпюру изгибающих моментов М х (рис. 24).
В сечении по оси симметрии рамы максимальные напряжения равны:
Момент сопротивления:
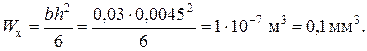
МПа.
