Дифференциальные уравнения плоскопараллельного движения твердого тела представляют собой совокупность уравнений поступательного движения плоской фигуры вместе с центром масс и вращательного движения относительно оси, проходящей через центр масс:
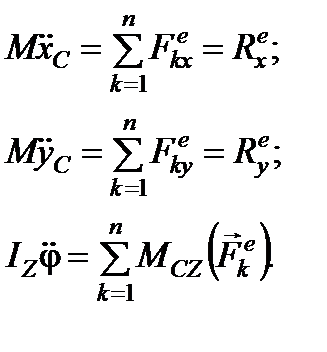
Пример:
Дано: r = 0,6 R,  ,
,  ,
,  , a=30о, b=60о.
, a=30о, b=60о.
|

|
| a |
|
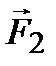
|
| О |
| В |
| у |
| х |
| b |
| С |
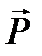
|
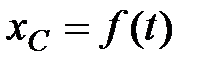 – закон движения центра масс,
– закон движения центра масс, 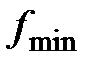 – наименьший коэффициент трения, при котором возможно качение без скольжения.
– наименьший коэффициент трения, при котором возможно качение без скольжения.
РЕШЕНИЕ:
Барабан совершает плоскопараллельное движение под действием сил  ,
, 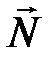 ,
, 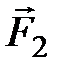 ,
, 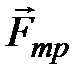 (направление
(направление 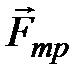 произвольно). Составим дифференциальные уравнения плоскопараллельного движения:
произвольно). Составим дифференциальные уравнения плоскопараллельного движения:
 ;
;  (1)
(1)
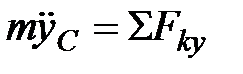 ;
; 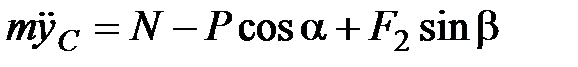 (2)
(2)
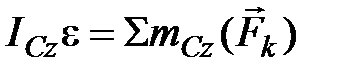 ;
;  (3)
(3)
(положительное направление моментов в направлении вращения барабана при его движении от т. О).
1) Определение  . В нашей задаче
. В нашей задаче  и
и 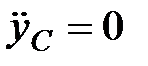 . Учтем, что
. Учтем, что 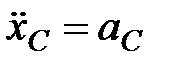 и при качении без скольжения в т. В находится мгновенный центр скоростей. Тогда
и при качении без скольжения в т. В находится мгновенный центр скоростей. Тогда
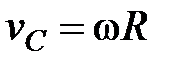 ,
,  или
или 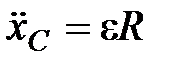 . (4)
. (4)
Тогда из уравнения (3)
 , (5)
, (5)
Сложив его почленно с (1) получим
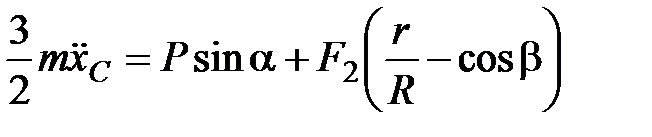 =
=  =
=  .
.
Отсюда, т.к. 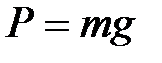 ,
, 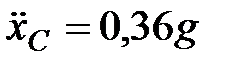 .
.
Интегрируем:
 и
и 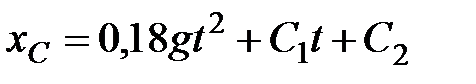 .
.
По начальным условиям при 
 и
и  получаем
получаем 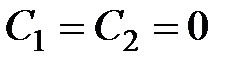 . Окончательно закон движения центра масс принимает вид
. Окончательно закон движения центра масс принимает вид
 .
.
2) Определение 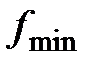 . При качении без скольжения сила трения должна удовлетворять неравенству
. При качении без скольжения сила трения должна удовлетворять неравенству
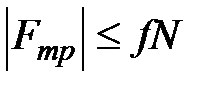 . (6)
. (6)
Из уравнения (2), учитывая, что 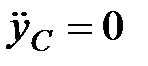 ,
,
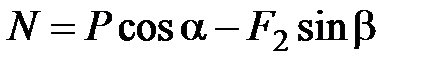 =
= 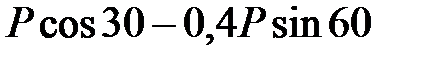 =
= 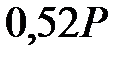
Из уравнения (5), учитывая, что 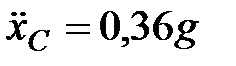
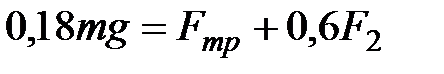 .
.
Отсюда, т.к. 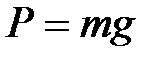 , то
, то 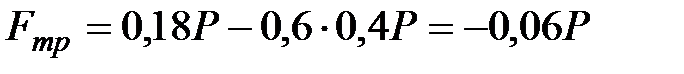
Подставим значения  и
и  в неравенство (6)
в неравенство (6) 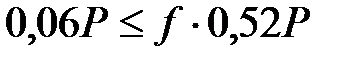 , откуда
, откуда 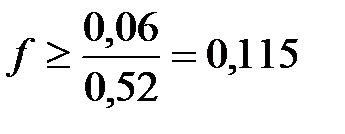 . Таким образом, наименьший коэффициент трения, при котором возможно качение барабана без скольжения
. Таким образом, наименьший коэффициент трения, при котором возможно качение барабана без скольжения
 .
.
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
 2020-10-11
2020-10-11 107
107








