В качестве исходного состояния (нулевого приближения) выбирается энергетический спектр свободного электрона 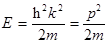 (рис. 7.2), а периодический потенциал кристаллической решетки
(рис. 7.2), а периодический потенциал кристаллической решетки  рассматривается как малое возмущение.
рассматривается как малое возмущение.
Исходное уравнение:
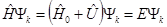
Из теории возмущений (без учета вырождения) поправки к энергии  первого порядка определяются диагональным матричным элементом матрицы оператора возмущений:
первого порядка определяются диагональным матричным элементом матрицы оператора возмущений:
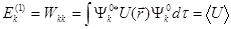 , (7.48)
, (7.48)
т.е. результат аналогичен приближению сильной связи, так как 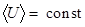 – это среднее значение оператора возмущений.
– это среднее значение оператора возмущений.
Поправка второго порядка:
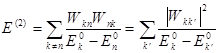 (7.49)
(7.49)
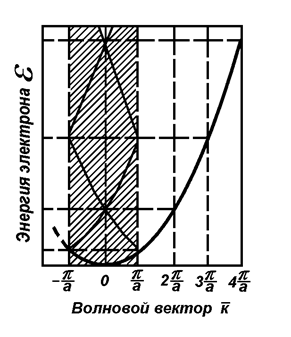
Рис. 7.2. Энергия свободного электрона в одномерном кристалле при равной нулю амплитуде периодического потенциала
С помощью этой поправки вычисляется поправка первого порядка волновой функции:
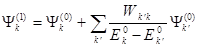 (7.50)
(7.50)
Недиагональные матричные элементы:
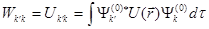 (7.51)
(7.51)
Чтобы найти явный вид матричных элементов оператора возмущения, представим 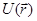 в виде разложения в ряд Фурье по обратной решетке:
в виде разложения в ряд Фурье по обратной решетке:
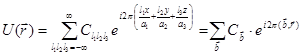 (7.52)
(7.52)
Для кубической решетки
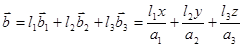
Недиагональный матричный элемент (7.51) в единице объема:
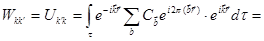
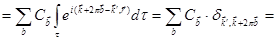
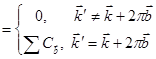 (7.53)
(7.53)
Таким образом, недиагональные матричные элементы могут быть равны нулю или 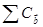 при
при 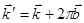 . Тогда поправка второго порядка:
. Тогда поправка второго порядка:
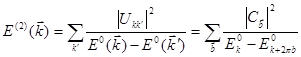 (7.54)
(7.54)
Волновая функция
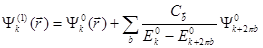 (7.55)
(7.55)
Эти условия означают, что вдали от особых точек 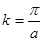 энергия электрона в кристалле не отличается от энергии свободного электрона и только в особых точках возмущение со стороны кристаллической решетки велико. Эти точки определяют границы зон Бриллюэна (рис. 7.3).
энергия электрона в кристалле не отличается от энергии свободного электрона и только в особых точках возмущение со стороны кристаллической решетки велико. Эти точки определяют границы зон Бриллюэна (рис. 7.3).
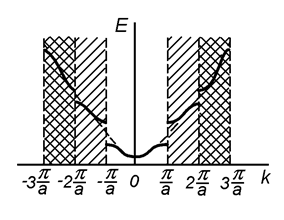
Рис. 7.3. Энергетический спектр электронов в кристалле в приближении слабой связи
Условие (7.55) соответствует вырождению, когда одному значению энергии соответствуют две волновые функции 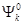 и
и 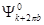 . Это означает, что уже в нулевом приближении необходимо учитывать обе волновые функции, т.е. рассматривать теорию возмущений с учетом вырождения. Нулевое приближение вырожденного состояния:
. Это означает, что уже в нулевом приближении необходимо учитывать обе волновые функции, т.е. рассматривать теорию возмущений с учетом вырождения. Нулевое приближение вырожденного состояния:
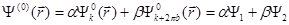 (7.56)
(7.56)
без вырождения b = 0.
Снова находим 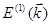 , но с учетом вырождения (7.56):
, но с учетом вырождения (7.56):
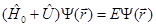 (7.57)
(7.57)
Обозначим 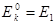 ,
, 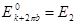 , с учетом вырождения (7.56) уравнение (7.57) имеет вид:
, с учетом вырождения (7.56) уравнение (7.57) имеет вид:
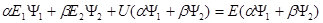 (7.58)
(7.58)
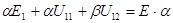
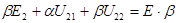 (7.59)
(7.59)
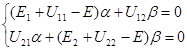 (7.60)
(7.60)
Нетривиальное решение системы (7.60) возможно, если детерминант равен нулю:
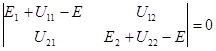 (7.61)
(7.61)
Учитывая U 11 = U 22 = <U> ® 0, из (7.61) имеем:
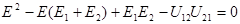 (7.62)
(7.62)
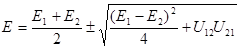 (7.63)
(7.63)
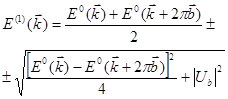 (7.64)
(7.64)
1. В первом приближении спектр энергии свободного электрона понижается на величину < U > без изменения зависимости 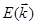 .
.
2. При наложении возмущения со стороны кристаллической решетки 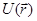 на свободное движение электрона энергия электрона
на свободное движение электрона энергия электрона 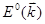 терпит разрыв на границах зоны Бриллюэна
терпит разрыв на границах зоны Бриллюэна 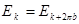 . В этих точках
. В этих точках 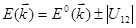 .
.
3. В результате разрыва энергии имеем зоны разрешенных и запрещенных энергий.
4. Все электрофизические свойства кристалла можно рассматривать в пределах первой зоны Бриллюэна.
 2020-10-10
2020-10-10 291
291








