2020-10-10
173
б) Как влияет граница зоны на движение электрона?
Выразим условие (7.66) через волну де-Бройля: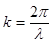 
, 
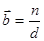(d – межплоскостное расстояние в кристалле).
(7.67)
После сокращения на l, d, p:
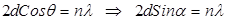, (7.68)
где q – угол падения;
a – угол скольжения.
Это совпадает с условием Вульфа-Бреггов для интерференции рентгеновских лучей.
Пусть a = 90°; 2 d = nl, т.е.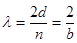 
. В этом случае 
.
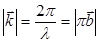Таким образом, при 
, т.е. когда значение 
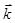соответствует границе зоны Бриллюэна, образуется стоячая волна, не переносящая энергию (за счет интерференции падающей и отраженной волн).
в) Как движется электрон в зоне Бриллюэна?
1. Вдали от границы зоны Бриллюэна зависимость Е от 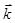мало отличается от зависимости для свободного электрона: 
, 
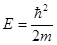. Групповая скорость электрона:
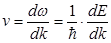(7.69)
Для свободного электрона скорость меняется от нуля до бесконечности монотонно. Наличие экстремумов приводит к уменьшению скорости на границе зоны Бриллюэна до нуля (рис. 7.6).
Рис. 7.6. Движение электрона в зоне Бриллюэна
2. Ускорение 
под действием силы 
: 
, с другой стороны:
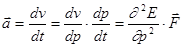(7.70)
Таким образом,
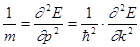(7.71)
Для свободного электрона m = Const = me.
В кристалле у минимума зоны Бриллюэна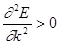 
, m * > 0, у максимума зоны Бриллюэна 
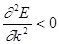, m * < 0 (рис.7.6 в).
Движение электрона в кристалле можно описать с помощью понятия эффективной массы m *, величина которой определяется кривизной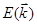 
– законом 
, а знак зависит от характера экстремума. При m * < 0 означает, что кристаллическая решетка влияет на движение электрона больше, чем внешняя сила F.
