Пусть Na = 0, т.е. донорный полупроводник (рис. 8.4):
no + nd – po = Nd (8.33)
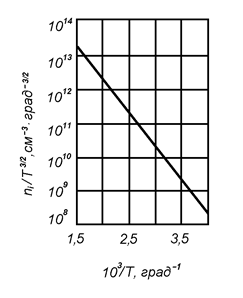
Рис. 8.7. Определение ширины запрещенной зоны из температурной зависимости концентрации электронов
1. Низкие температуры (po = 0), до начала собственной проводимости
no + nd = Nd
no = Nd – nd = pd (8.34)
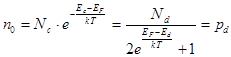 (8.35)
(8.35)
Обозначим 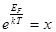 :
:
 (8.36)
(8.36)

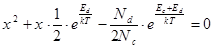 (8.37)
(8.37)
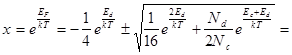
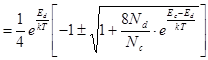 (8.38)
(8.38)
Оставим плюс, так как x > 0.
 (8.39)
(8.39)
Проанализируем (8.39).
1. 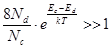 , температуры вблизи 0 К.
, температуры вблизи 0 К.
Тогда можно пренебречь в (8.39) единицей под радикалом и в квадратных скобках:
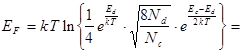
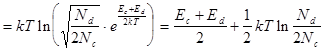 (8.40)
(8.40)
Если T = 0, то 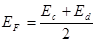
С ростом Т уровень Ферми поднимается, так как Nd > 2 Nc, a Nc ~  , и проходит через максимум, а затем понижается, пересекая
, и проходит через максимум, а затем понижается, пересекая 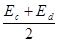 при 2 Nc = Nd (рис. 8.8). В этом интервале температур, где работает формула (8.40), концентрация электронов:
при 2 Nc = Nd (рис. 8.8). В этом интервале температур, где работает формула (8.40), концентрация электронов:
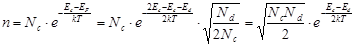 (8.41)
(8.41)
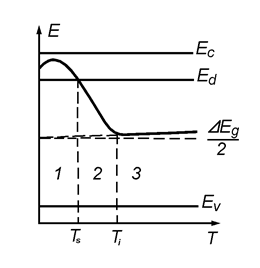
Рис. 8.8. Температурная зависимость положения уровня Ферми
Таким образом, из температурной зависимости 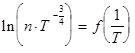 можно найти энергию активации донорного уровня:
можно найти энергию активации донорного уровня:  (рис. 8.9(1)).
(рис. 8.9(1)).
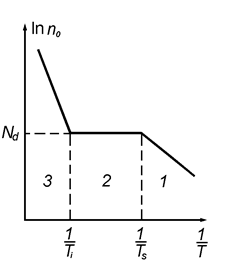
Рис. 8.9. Температурная зависимость концентрации носителей заряда в донорном полупроводнике
2. Более высокие Т:  , также Nc >>8 Nd.
, также Nc >>8 Nd.
Разлагая радикал в (8.39) в ряд и ограничиваясь первым членом разложения:
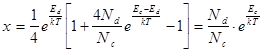 , (8.42)
, (8.42)
так как Nc > Nd:
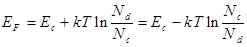 (8.43)
(8.43)
С ростом Т уровень Ферми удаляется (опускается) от Ес. Концентрация электронов:
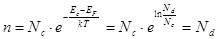 , (8.44)
, (8.44)
т.е. n ¹ f (T) и равна концентрации примеси – все примесные уровни ионизованы. Это истощение (рис. 8.8(2)).
В этой области можно определить концентрацию примесных атомов (рис. 8.9(2)). В области истощения резко возрастает концентрация неосновных носителей заряда:
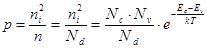 (8.45)
(8.45)
3. Высокие температуры
Дырок много, а донорный уровень истощен 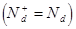 . Исходное уравнение:
. Исходное уравнение:
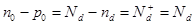 (8.46)
(8.46)
Так как  , то
, то
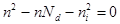 (8.47)
(8.47)
 (8.48)
(8.48)
Оставим плюс, учтем 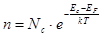 и
и 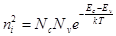 , получаем
, получаем
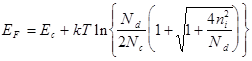 (8.49)
(8.49)
1. Не очень высокие Т: 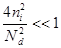 , т.е.
, т.е. 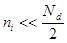
Так как n = Nd, то  .
.
Из (8.49):
 , (8.50)
, (8.50)
что совпадает с (8.43), т.е. область истощения примеси.
2. Очень высокие Т:  , т.е.
, т.е. 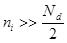
Из (17): n = ni, из (18):
 , (8.51)
, (8.51)
т.е. аналогично собственному полупроводнику (рис. 8.8(3)).
Из зависимости 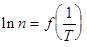 можно определить D Еg и Еi (рис. 8.9).
можно определить D Еg и Еi (рис. 8.9).
 2020-10-10
2020-10-10 185
185








