Определение: Рациональная дробь называется правильной, если степень многочлена в числителе меньше степени многочлена в знаменателе. В противном случае рациональная дробь называется неправильной.
Выделяя из неправильной дроби ее целую часть (путем деления числителя на знаменатель), всегда можно представить ее в виде суммы многочлена и правильной рациональной дроби.
Разложение конкретной правильной рациональной дроби 
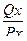 на сумму элементарных дробей обычно производят методом неопределенных коэффициентов. Для этого разлагают знаменатель
на сумму элементарных дробей обычно производят методом неопределенных коэффициентов. Для этого разлагают знаменатель 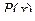 на произведение линейных и квадратичных множителей, представляют данную дробь в виде суммы дробей с неопределенными коэффициентами в числителях. Затем приводят элементарные дроби к общему знаменателю
на произведение линейных и квадратичных множителей, представляют данную дробь в виде суммы дробей с неопределенными коэффициентами в числителях. Затем приводят элементарные дроби к общему знаменателю 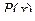 и приравнивают многочлен, получившийся в числителе, многочлену
и приравнивают многочлен, получившийся в числителе, многочлену  .
.
Для того чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы коэффициенты при одинаковых степенях  у них были равны. Получаем тем самым систему алгебраических уравнений для нахождения неопределенных коэффициентов.
у них были равны. Получаем тем самым систему алгебраических уравнений для нахождения неопределенных коэффициентов.
Пример 10.
Найти интеграл 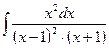
Запишем подинтегральную функцию в виде суммы простейших дробей и приведем к общему знаменателю, имеем
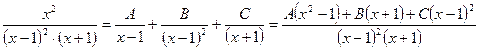
Раскрываем скобки и приравниваем коэффициенты при одинаковых степенях
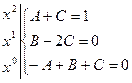
Решая эту систему, находим:
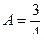 ,
, 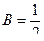 ,
, 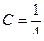
отсюда: 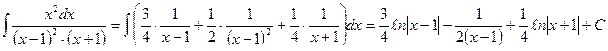
Интегрирование тригонометрических выражений
Определение: Рациональной функцией относительно 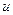 и
и 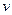 называется отношение двух многочленов относительно
называется отношение двух многочленов относительно 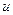 и
и 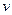 .
.
В дальнейшем символом 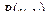 будем обозначать рациональную функцию относительно переменных
будем обозначать рациональную функцию относительно переменных 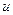 и
и 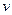 . Будем говорить, что функция
. Будем говорить, что функция 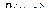 – нечетная относительно
– нечетная относительно 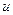 , если при замене
, если при замене 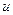 на
на 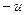 функция
функция 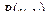 меняет знак, т.е.
меняет знак, т.е. 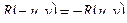 . Если
. Если 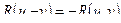 , то будем говорить, что такая функция нечетна относительно
, то будем говорить, что такая функция нечетна относительно 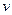 .
.
Функция 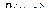 четна относительно
четна относительно 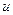 и
и 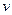 , если при одновременной замене
, если при одновременной замене 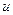 на
на 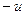 ,
, 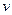 на
на 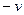 функция не изменяется, т.е.
функция не изменяется, т.е. 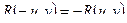 .
.
Заметим, что любая тригонометрическая функция аргумента  рационально выражается через тангенс половинного угла. Действительно,
рационально выражается через тангенс половинного угла. Действительно,
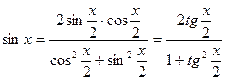
 ,
,
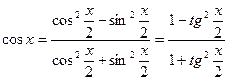 , а так как
, а так как  ,
, 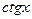 ,
,  ,
, 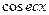 рационально выражаются через
рационально выражаются через 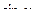 и
и 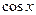 , то они рационально будут выражаться и через
, то они рационально будут выражаться и через 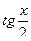 .
.
Теорема 1. Интеграл вида 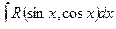 подстановкой
подстановкой 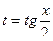 приводится к интегралу от рациональной функции
приводится к интегралу от рациональной функции 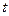 , который, как было указано выше, всегда выражается в элементарных функциях.
, который, как было указано выше, всегда выражается в элементарных функциях.
Пусть 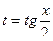 , тогда
, тогда 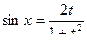 ,
, 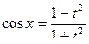 ,
,  ,
, 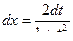
Данная подстановка называется универсальной подстановкой.
Применим универсальную подстановку 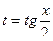
Пример 11.
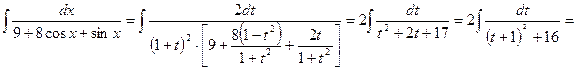
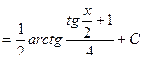 .
.
Теорема 2. Если функция  нечетна относительно
нечетна относительно 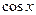 , то интеграл
, то интеграл 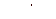 подстановкой
подстановкой 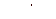 приводится к интегралу от рациональной функции.
приводится к интегралу от рациональной функции.
Теорема 3. Если 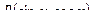 имеет нечетный характер относительно
имеет нечетный характер относительно 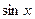 , то подстановкой
, то подстановкой 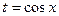 интеграл
интеграл 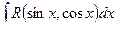 приводится к интегралу от рациональной функции.
приводится к интегралу от рациональной функции.
Пример 12.
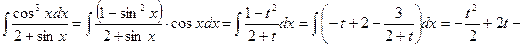
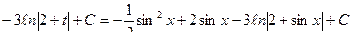 .
.
Подинтегральная функция нечетна относительно 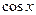 . Применим подстановку
. Применим подстановку 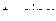 , тогда
, тогда 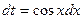 .
.
Пример 13.
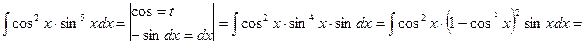
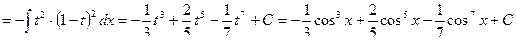 .
.
Теорема 4. Если 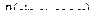 имеет четный характер относительно
имеет четный характер относительно 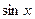 и
и 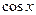 , то интеграл
, то интеграл 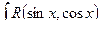 подстановкой
подстановкой  приводится к интегралу от рациональной функции.
приводится к интегралу от рациональной функции.
Пример 14.
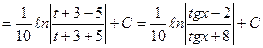 .
.
На практике при интегрировании тригонометрических функций часто еще используют известные формулы тригонометрии:
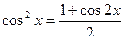 ,
,
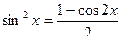 ,
,
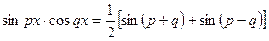 ,
,
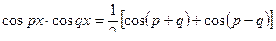 ,
,
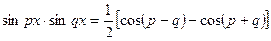 , и другие.
, и другие.
Пример 15.
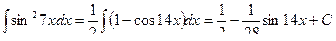 .
.
Пример 16.
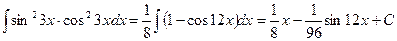 .
.
Пример 17.
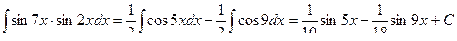 .
.
Интегрирование иррациональных функций
Простейшие интегралы от функций, содержащие иррациональности, являются табличными, либо сводятся к табличным с использованием свойств интеграла и замены переменной. В более сложных случаях основной подход состоит в сведении искомого интеграла к интегралу от рациональной функции с помощью подходящей замены переменной.
Теорема 1. Интеграл вида 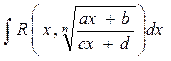 , где
, где 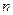 – натуральное число подстановкой
– натуральное число подстановкой 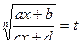 приводится к интегралу от рациональной функции
приводится к интегралу от рациональной функции 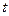 или, как говорят, «рационализируется».
или, как говорят, «рационализируется».
Следствие. Интеграл вида 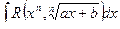 подстановкой
подстановкой 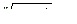 рационализируется.
рационализируется.
Найти интегралы:
Пример 18.
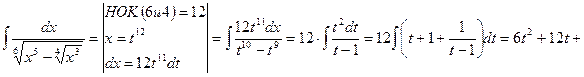
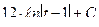 , где
, где 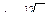 .
.
Пример 19.
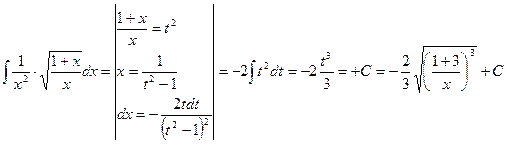 .
.
Интегралы вида 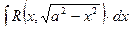 ,
, 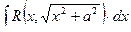 ,
, 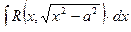 , где
, где 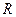 – рациональная функция, находятся с помощью подстановок
– рациональная функция, находятся с помощью подстановок 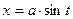 ,
, 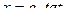 ,
, 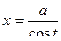 .
.
 2020-10-12
2020-10-12 185
185








