Свойство 1. Постоянный множитель 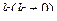 можно выносить за знак интеграла:
можно выносить за знак интеграла: 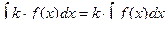 .
.
Свойство 2. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций: 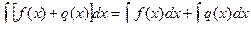 .
.
Свойство 3. 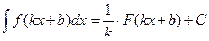 , где
, где 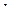 ,
, 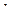 – числа,
– числа, 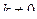 .
.
Приведем таблицу основных интегралов. Часть формул этой таблицы непосредственно следует из определения интегрирования как операции, обратной дифференцированию, и таблицы производных.
1. 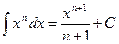 , где
, где 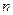 – действительное число,
– действительное число,  ,
,
2. 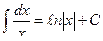 ,
,
3. 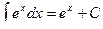 ,
,
4. 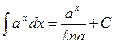 ,
,
5. 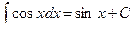 ,
,
6. 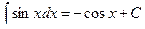 ,
,
7. 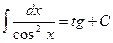 ,
,
8. 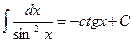 ,
,
9. 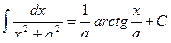 ,
, 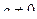 ,
,
10. 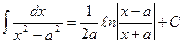 ,
, 
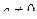 ,
,
11. 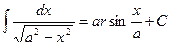 ,
, 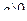 ,
,
12. 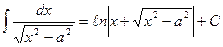 ,
, 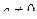 ,
,
13. 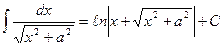 ,
, 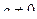 ,
,
14. 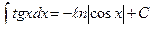 ,
, 
15. 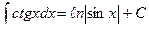 .
. 
Основные приемы интегрирования
Используя свойства неопределенных интегралов и таблицу основных интегралов, можно интегрировать некоторые элементарные функции (так называемое непосредственное интегрирование).
Рассмотрим несколько примеров.
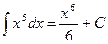 ,
,
 ,
,
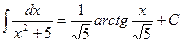 ,
,
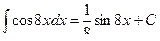 ,
,
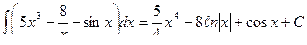 ,
,
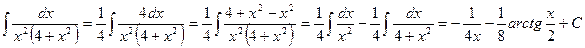 .
.
Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла. Такой метод называется методом подстановки, а также методом переменной.
Рассмотрим функцию 
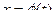 , где
, где 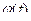 – строго монотонная и непрерывно дифференцируемая функция на некотором промежутке. Если на соответствующем промежутке изменения
– строго монотонная и непрерывно дифференцируемая функция на некотором промежутке. Если на соответствующем промежутке изменения  функция интегрируема, то
функция интегрируема, то 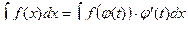 (1)
(1)
После нахождения интеграла 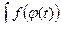
 надо вместо
надо вместо 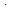 подставить его выражение через
подставить его выражение через  .
.
Рассмотрим несколько примеров.
Пример 1. 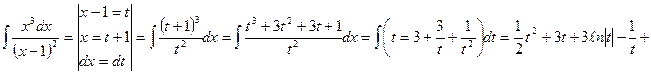
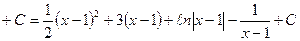
Замена переменной в неопределенном интеграле чаще производится по формуле (1), прочитанной справа налево:

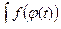
 , где
, где 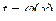
Пример 2.
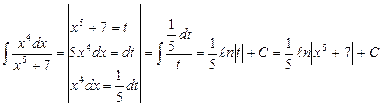

Пример 3.
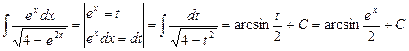
 2020-10-12
2020-10-12 174
174








