Пусть 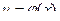 и
и 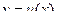 непрерывно дифференцируемы на некотором промежутке. Тогда
непрерывно дифференцируемы на некотором промежутке. Тогда 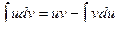 . Эта формула называется формулой интегрирования по частям. Правильнее было бы назвать ее формулой частичного интегрирования. При известных
. Эта формула называется формулой интегрирования по частям. Правильнее было бы назвать ее формулой частичного интегрирования. При известных 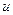 и
и 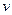 она сводит нахождение интеграла от
она сводит нахождение интеграла от 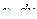 после частичного интегрирования к нахождению интеграла от
после частичного интегрирования к нахождению интеграла от 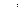 .
.
Сущностью метода интегрирования по частям главным является разумное разбиение подинтегрального выражения на множители 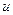 и
и 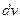 . Общих установок по этому вопросу нет. Однако для некоторых типов интегралов, сделать это возможно.
. Общих установок по этому вопросу нет. Однако для некоторых типов интегралов, сделать это возможно.
I тип. В интегралах вида 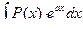 ,
, 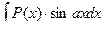 ,
, 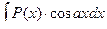 , где
, где 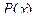 – многочлен относительно
– многочлен относительно  ,
, 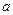 – число за
– число за 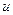 берут
берут 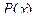 , все остальные множители обозначают
, все остальные множители обозначают 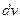 .
.
II тип. В интегралах вида 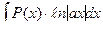 ,
, 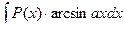 ,
, 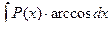 ,
, 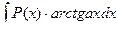 ,
, 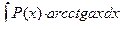 полагают
полагают 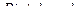 , все остальные за
, все остальные за 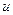 .
.
III тип. В интегралах вида 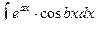 ,
, 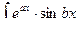 , где
, где 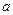 и
и  – числа можно принять за
– числа можно принять за 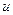 любую функцию или
любую функцию или 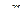 или
или 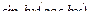 .
.
Пример 4.
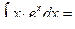
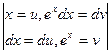

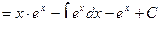
Пример 5.
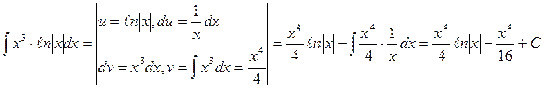
Иногда для получения окончательного результата приходится несколько раз последовательно применять формулу интегрирования по частям.
Пример 6.
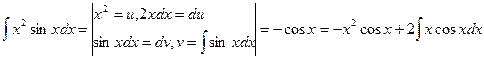
Вычислим 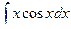 отдельно, используя формулу интегрирования по частям
отдельно, используя формулу интегрирования по частям
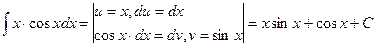
Окончательно получаем:
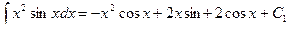 , где
, где 
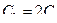
Нахождение некоторых интегралов методом интегрирования по частям сводится к решению алгебраического уравнения, в котором неизвестным является искомый интеграл. Это относится к вычислению интегралов III типа.
Пример 7.
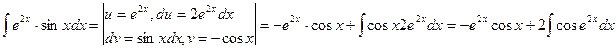 Вычислим отдельно
Вычислим отдельно 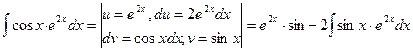
Подставим полученное выражение в искомое: 
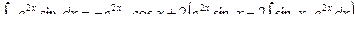
Раскрыв скобки, приведя подобные слагаемые, получим
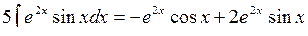 , отсюда
, отсюда 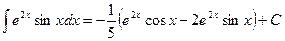 .
.
Общие приемы интегрирования
Интегрирование элементарных функций
Элементарными дробями называются дроби следующих четырех типов:
I) 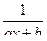 II)
II) 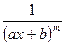 III)
III) 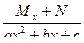 IV)
IV) 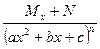 , где
, где  и
и 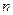 – натуральные числа,
– натуральные числа,  ,
, 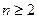 ,
, 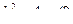 .
.
Интегралы I) 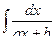 и II)
и II) 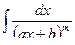 подстановкой
подстановкой 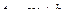 сводятся к табличным интегралам:
сводятся к табличным интегралам:
I. 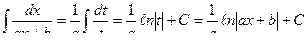 ,
,
II. 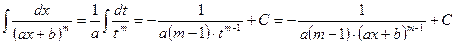 .
.
Интегралы III) 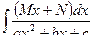 и IV)
и IV) 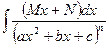 также сводятся к табличным, путем более сложных (в техническом плане) упражнений и подстановок.
также сводятся к табличным, путем более сложных (в техническом плане) упражнений и подстановок.
Пример 8.
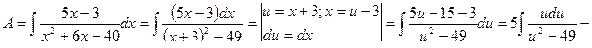
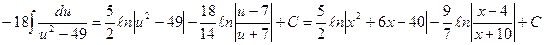
Пример 9.
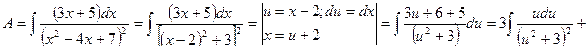
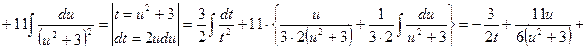
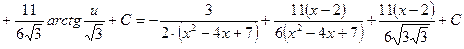
 2020-10-12
2020-10-12 180
180








