2020-10-12
126
Общий вид дифференциального уравнения первого порядка: 
.
Если это соотношение разрешить относительно 
, то получится уравнение вида: 
. Оно называется дифференциальным уравнением первого порядка, разрешенным относительно производной. Его всегда можно записать в так называемой дифференциальной форме: 
или .
Отыскание решения дифференциального уравнения , которое удовлетворяет заданным начальным условиям 
, является одной из важнейших задач теории дифференциальных уравнений. Эта задача называется задачей Коши.
Уравнения с разделяющимися переменными
Определение: Дифференциальное уравнение называется уравнением с разделяющимися переменными, если его можно записать в виде: 
, то есть, если его правая часть есть произведение двух функций, одна из которых не зависит от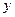 
, а другая от 
.
Пример 1.
Найти общее решение дифференциального уравнения 
. 
Разделяя переменные 
и интегрируя, получаем: 
– общий интеграл данного уравнения во всей плоскости 
.
Пример 2.
Решить дифференциальное уравнение 
и найти частное решение, удовлетворяющее начальному условию 
.
Уравнение является уравнением с разделяющимися переменными. Приведем его к виду: 
.
Если равны дифференциалы, то равны неопределенные интегралы 
. Отсюда получаем 
Общий интеграл 
. Подставляем начальное условие : 
,
отсюда получаем частный интеграл 
