Определение: Функция 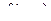 называется однородной
называется однородной 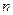 -го измерения относительно своих аргументов
-го измерения относительно своих аргументов  и
и 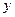 , если для любого
, если для любого 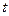 имеет место тождество
имеет место тождество 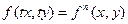 .
.
Например,  однородная функция 3го измерения относительно
однородная функция 3го измерения относительно  и
и 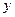 , т.к.
, т.к. 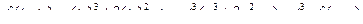 .
.
Сумма однородных функций одинакового измерения есть однородная функция того же измерения.
Произведение однородных функций есть однородная функция, измерение которой равно сумме измерений сомножителей.
Частное однородных функций есть однородная функция. Её измерение равно разности измерений делимого и делителя.
Определение: Дифференциальное уравнение  называется однородным, если его правая часть
называется однородным, если его правая часть 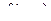 есть однородная функция нулевого измерения относительно своих аргументов. Однородным будет также всякое уравнение вида:
есть однородная функция нулевого измерения относительно своих аргументов. Однородным будет также всякое уравнение вида: 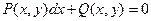 , где
, где 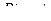 и
и 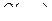 – однородные функции одинакового измерения.
– однородные функции одинакового измерения.
С помощью замены 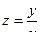 , где
, где 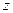 – новая неизвестная функция, однородное дифференциальное уравнение сводится к уравнению с разделяющимися переменными.
– новая неизвестная функция, однородное дифференциальное уравнение сводится к уравнению с разделяющимися переменными.
Пример 3.
Найти общее решение уравнения 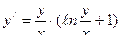 .
.
Функция 
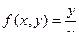
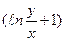 определена в областях где
определена в областях где 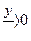 , т.е.
, т.е. 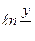 имеет смысл. Полагаем
имеет смысл. Полагаем 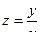 ,
, 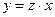 . При этом
. При этом 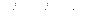 .
.
Получаем уравнение с разделяющимися переменными относительно 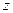 :
:
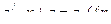
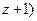 ,
,

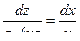
Интегрируем левую часть по 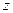 , правую по
, правую по  ; получаем
; получаем 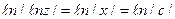 ,
, 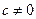 ,
,
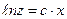

Подставляя 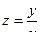 , находим
, находим  – совокупность решений данного уравнения. Здесь
– совокупность решений данного уравнения. Здесь 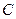 – любое отличное от нуля число.
– любое отличное от нуля число.
Линейные уравнения
Определение: Дифференциальное уравнение 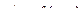 называется линейным, если оно линейно относительно искомой функции
называется линейным, если оно линейно относительно искомой функции 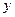 и её производной
и её производной  , т.е. оно может быть записано в виде:
, т.е. оно может быть записано в виде:  (1).
(1).
Если в этом уравнении правая часть 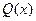 не равна тождественно нулю, то это уравнение называется линейным неоднородным уравнением. Если же
не равна тождественно нулю, то это уравнение называется линейным неоднородным уравнением. Если же 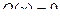 , то уравнение называется линейным однородным уравнением.
, то уравнение называется линейным однородным уравнением.
Рассмотрим сначала линейное однородное уравнение 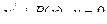 . Это уравнение с разделяющимися переменными. Разделяя переменные и интегрируя, находим:
. Это уравнение с разделяющимися переменными. Разделяя переменные и интегрируя, находим: 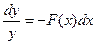 ,
,
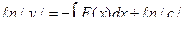 ,
,
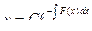 , где
, где 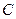 – произвольная постоянная, отличная от нуля.
– произвольная постоянная, отличная от нуля.
Для отыскания решений линейного неоднородного уравнения применим метод вариации произвольной постоянной.
Выполним замену 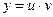 , где u и
, где u и 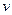 – новые функции от
– новые функции от  . Тогда уравнение (1) примет вид:
. Тогда уравнение (1) примет вид:

 ,
,

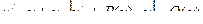 .
.
Если потребовать, чтобы выражение в квадратных скобках было равно 0, т.е. 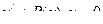 , но найдем сначала
, но найдем сначала 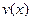 , а затем
, а затем 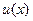 , а, следовательно, найдем
, а, следовательно, найдем 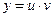 .
.
Пример 4.
Решить дифференциальные уравнения:
а) 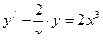 Это линейное уравнение первого порядка
Это линейное уравнение первого порядка 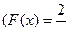 ;
;  .
.
Выполним замену 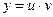
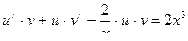 ,
,
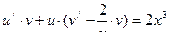 .
.
Приравнивая к нулю выражение в скобках, получаем 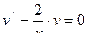
 – уравнение с разделяющимися переменными.
– уравнение с разделяющимися переменными.



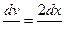 отсюда
отсюда 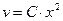
Подставляя 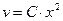 в исходное уравнение. Находим
в исходное уравнение. Находим 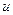 :
:
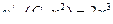 ,
,
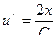 отсюда
отсюда 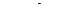 , где
, где  – произвольная постоянная.
– произвольная постоянная.
Получаем общее решение уравнения:
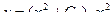
б) 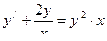
Сделав замену 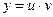 , получим
, получим
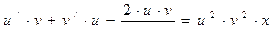
Сгруппируем второе слагаемое с третьим:
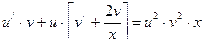
Приравниваем к  в квадратных скобках, находим функцию
в квадратных скобках, находим функцию 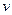 :
:
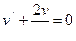 ;
;
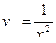
Подставим 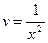 , находим
, находим 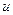 :
:
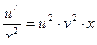 ,
,
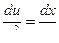 ;
; 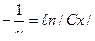 ,
,
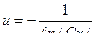 отсюда
отсюда 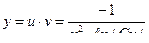
Уравнения 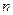 -го порядка, допускающие понижение порядка
-го порядка, допускающие понижение порядка
Для решения уравнения  сделаем замену
сделаем замену
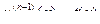 ,
, 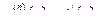
Пример 5.
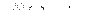
Заменим  , получим
, получим
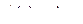 , отсюда
, отсюда 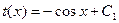 , т.е.
, т.е. 
Повторив еще трижды замену, найдем 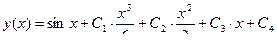
 2020-10-12
2020-10-12 260
260








