Второго порядка с постоянными коэффициентами

Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид , где 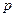,  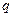– некоторые действительные числа,  – некоторая функция. Если  тождественно равна нулю, то соответствующее уравнение называется однородным, в противном случае – неоднородным.

Рассмотрим решение однородного дифференциального уравнения . Ему ставится в соответствие характеристическое уравнени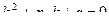е: , где  переменная.

Если характеристическое уравнение имеет действительные корн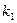и  и , причем 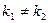, то общее решение уравнения имеет вид: .

Если характеристическое уравнение имеет один корень (кратности 2), то общее решение уравнения имеет вид: .

Если характеристическое уравнение имеет комплексные корни , то общее решение уравнения имеет вид:

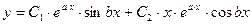, где 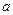,  – действительные числа.

Пример 6:

Найти общие решения дифференциальных уравнений:

а)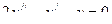

Составим характеристическое уравнение

, ,

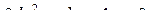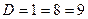Уравнение имеет два различных корня

, .

Общее решение дифференциального уравнения имеет вид:

.

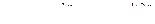б)

Уравнение имеет два совпадающих корня или один корень кратности 2, 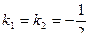, поэтому искомое общее решение дифференциального уравнения есть .

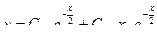в)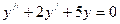

Характеристическое уравнение будет

, .

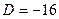Уравнение имеет комплексные корни , поэтому общее решение дифференциального уравнения имеет вид

.

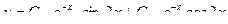Рассмотрим решение неоднородного дифференциального уравнения. Один из способов решения уравнения основан на том, что общее решение неоднородного дифференциального уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения исходного однородного уравнения.

Пример 7

Найти частные решения неоднородных уравнений:

Напишем характеристический многочлен 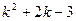. Его корнями являются числа  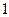и .

Так как 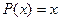 и, можно полагать, 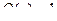, поэтому частное решение будем искать в виде . Подставляя эту функцию в исходное уравнение, после приведения подобных слагаемых и сохранения на приходим к равенству , которое удовлетворяется тождественно (при всех ), если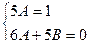

Откуда 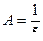,  и искомое частное решение имеет вид: .

Пример 8

Найти общее решение уравнения:

Решение:

Найдём корни характеристического уравнения: , тогда

, , тогда фундаментальную систему решений образуют функции:

   

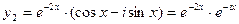
Так как действительные мнимые решения в отдельности являются решениями уравнения, то в качестве линейно независимых частей решений  и , возьмем , , тогда общее решение однородного уравнения будет иметь вид: 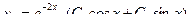. Представим правую часть уравнения, как  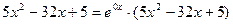и сравним с выражением, задающим правую часть специального вида:

 

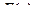
Имеем 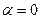, , 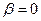тогда т.к.  – многочлен второй степени, то общий вид правой части: .

Найдем частные решения:

 , ,     

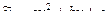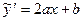Сравним коэффициенты при  слева и справа, найдем 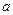, , 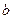, решив систему:    ,

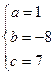отсюда .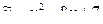

Тогда общее решение заданного неоднородного линейного уравнения имеет вид:

.

Таким образом, при решении линейного однородного дифференциального уравнения второго порядка возможны три случая решения характеристического уравнения.