Ряды с отрицательными, точнее, с неположительными членами отличаются от соответствующих рядов с неотрицательными членами только множителем 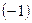 , и вследствие этого такие ряды ведут себя одинаково относительно сходимости.
, и вследствие этого такие ряды ведут себя одинаково относительно сходимости.
Рассмотрим признаки сходимости рядов с неотрицательными членами.
Первый признак сравнения рядов с неотрицательными членами:
Пусть даны два ряда с неотрицательными членами 
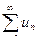 (1) и
(1) и 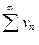 (2)
(2)  ,
,  . Если
. Если 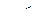 при любом
при любом 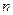 , то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда (2).
, то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда (2).
Пример 3. Ряд 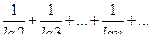 расходится, т.к.
расходится, т.к. 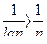 , а гармонический ряд
, а гармонический ряд 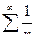 расходится. В частности при
расходится. В частности при 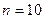 имеем
имеем 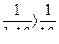 ,
, 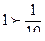
Пример 4. Ряд 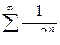 сходится, т.к. сходится ряд геометрической прогрессии
сходится, т.к. сходится ряд геометрической прогрессии 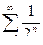 , а члены данного ряда не больше соответствующих членов этого ряда сходящейся геометрической прогрессии:
, а члены данного ряда не больше соответствующих членов этого ряда сходящейся геометрической прогрессии: 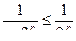 .
.
В частности, при 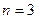 имеем
имеем 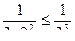 ,
, 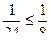 .
.
Второй признак сравнения рядов:
Пусть даны 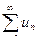 и
и 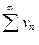 , где
, где  ,
, 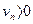 . Если существует
. Если существует 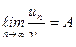 , где
, где 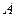 – число, отличное от нуля, то ряды
– число, отличное от нуля, то ряды 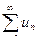 и
и 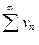 ведут себя одинаково относительно сходимости.
ведут себя одинаково относительно сходимости.
Признак Даламбера (предельный признак Даламбера):
Пусть дан ряд 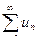 ,
,  . Если существует
. Если существует 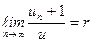 , то при
, то при  ряд сходится, при
ряд сходится, при  ряд расходится, при
ряд расходится, при 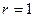 признак вопроса не решает.
признак вопроса не решает.
Пример 5. Ряд 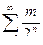 сходится, т.к.
сходится, т.к. 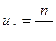 ,
, 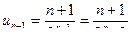
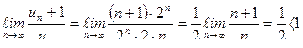 .
.
Пример 6. Ряд 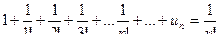 ,
, 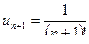 ,
, 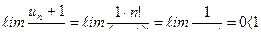 .
.
Пример 7. Ряд 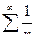 расходится.
расходится. 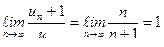 . По признаку Даламбера в этом случае требуется дополнительное исследование. Это будет показано далее, по интегральному признаку сравнения.
. По признаку Даламбера в этом случае требуется дополнительное исследование. Это будет показано далее, по интегральному признаку сравнения.
Признак Коши:
Пусть дан 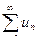 ,
,  . Если существует
. Если существует 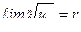 , то при
, то при 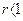 ряд сходится, при
ряд сходится, при  ряд расходится, при
ряд расходится, при 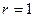 признак вопроса не решает.
признак вопроса не решает.
Пример 8. Ряд 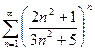 сходится, т.к.
сходится, т.к. 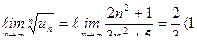 .
.
Пример 9. Рассмотрим ряд 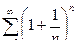 .Найдём
.Найдём 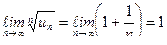 .
.
Вопрос о сходимости данного ряда признаком Коши не решается. Хотя с учетом второго замечательного предела имеем, что 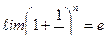 , значит ряд расходится.
, значит ряд расходится.
Интегральный признак сходимости рядов
с положительными членами:
Если 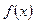 – непрерывная положительная убывающая функция на промежутке
– непрерывная положительная убывающая функция на промежутке  , то ряд
, то ряд 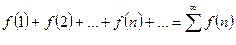 и интеграл
и интеграл 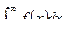 ведут себя одинаково относительно сходимости.
ведут себя одинаково относительно сходимости.
Пример 10. Рассмотрим ряд 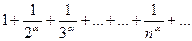 При
При 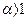
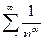
сходится, так как 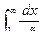 сходится, при
сходится, при 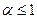
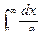 расходится.
расходится.
В частности, при 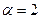 получим сходящийся ряд
получим сходящийся ряд 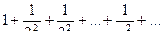 , т.к.
, т.к.
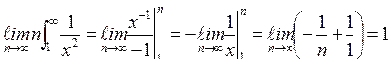 .
.
При 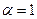 получим известный расходящийся гармоничный ряд
получим известный расходящийся гармоничный ряд 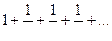 .
.
Рассмотрим 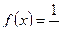 ,
, 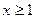
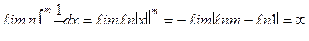 .
.
 2020-10-12
2020-10-12 180
180








