2020-10-12
96
Суммой 
двух векторов 
и 
называется вектор, который получается из векторов
и по правилу треугольника или по правилу параллелограмма:
Операция сложения векторов обладает следующими свойствами:
1.Сложение векторов коммутативно: 
2.Сложение векторов ассоциативно: 
3.Для любых двух векторов имеет место неравенство треугольника:
£ 
Вектор, равный вектору 
по длине и противоположно направленный, называется противоположным вектором для вектора и обозначается 
.
Разностью 
векторов и 
называется сумма векторов и 
, т. е. 
Произведением вектора на действительное число 
называется вектор 
, длина которого 
, а направление совпадает с направлением вектора , если 
и противоположно ему, если 
.
Из определения произведения вектора на число, следует, что два вектора 
и 
коллинеарны тогда и только тогда, когда имеет место равенство: 
.
Операция умножения вектора на число обладает следующими свойствами:
l,mÎR
1) l(m 
|
|
|
2) 
3) 
Если 
, то
,
,
.
Признаком коллинеарности двух векторов и 
является пропорциональность их координат: 
.
Пример 1.
Даны векторы 
и l=3.
Найти 
Решение. Пользуясь свойствами суммы,разности векторов и произведения вектора на число, получаем:
Пример 2.
Коллинеарны ли векторы 
Решение.
т.к. соответствующие координаты не пропорциональны, то векторы не коллинеарны.
Упражнения.
1. По данным векторам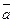 
и 
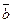построить каждый из следующих векторов:
1) 
; 2) 
; 3) 
; 4) 
.
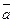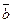2. По данным векторам и построить каждый из следующих векторов:
1) 
; 2) 
; 3) 
; 4) 
.
3. Проверить коллинеарность векторов 
и 
. Установить какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны.
4. Даны точки 
и 
. Проверить, что векторы 
и 
коллинеарны.
§ 5. Скалярное произведение векторов.
Скалярным произведение двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
Скалярное произведение векторов 
и 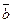обозначается символом 
.
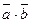Если угол между векторам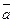и и 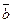обозначить через 
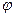, то их скалярное произведение можно выразить формулой
. (1)
Скалярное произведение векторов 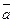, 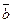можно выразить также формулой
, или 
.
Из формулы (1) следует, что 
, если 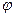- острый угол, 
, если 
- тупой; 
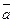в том и только в том случае, когда векторы и 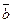перпендикулярны.
Скалярное произведение 
называется скалярным квадратом вектора и обозначается символом 
. Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля:
|
|
|
.
Пусть векторы 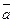и 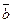заданы своими координатами:
, 
.
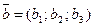Найдем их скалярное произведение:
так как 
как скалярные квадраты единичных векторов;
как скалярные произведения взаимно перпендикулярных векторов, то окончательно имеем:
.
Отсюда следует необходимое и достаточное условие перпендикулярности векторов:
.
Угол 
между векторами 
и 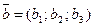находится по формуле
,
или в координатах
.
