Температура Кюри. Теория среднего поля

Рассмотренное выше упорядоченное расположение магнитных моментов является идеализированным, поскольку не учитывает тепловое движение атомов, которое неизбежно приводит к некоторым нарушениям упорядоченного расположения магнитных моментов. При сравнительно низких температурах они незначительны, при увеличении температуры, они играют все большую роль, и, наконец, при некоторой температуре, называемой температурой Кюри (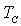), тепловое движение атомов способно разрушить упорядоченное расположение магнитных моментов, и тогда ферромагнетик превращается в парамагнетик. Величина 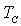зависит от прочности связи магнитных моментов друг с другом, в случае прочной связи 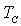достигает 770 ⁰С - для железа и превышает 1000 ⁰С для железо-кобальтовых сплавов. Для многих веществ 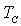невелика и составляет менее 300 К.

По величине 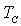можно оценить энергию связи 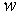магнитных моментов друг с другом. Для разрушения упорядоченного расположения магнитных моментов необходима энергия теплового движения порядка эВ. Это - очень большая величина, намного превосходящая как энергию взаимодействия диполей, так и потенциальную энергию магнитного диполя в поле . В самом деле, энергия взаимодействия диполя находящегося в поле по порядку величины составляет 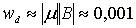эВ, что значительно меньше, чем . Следовательно, ее недостаточно для сохранения упорядоченного расположения магнитных моментов при температуре порядка 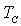. Поэтому рассмотренное выше квантовое объяснение магнитного упорядочения, связанного с электростатическим взаимодействием электронных оболочек, является единственным удовлетворительным и общепризнанным. Тем не менее, часто используют классические модели, в основе которых лежит "чисто магнитная" природа магнитного упорядочения. Эти модели удачно предсказывают поведение магнетика вблизи , хотя и основаны на не вполне корректных предположениях; рассмотрим наиболее удачные из них.

Модель среднего поля. Некоторые модели, удачно описывающие многие свойства ферромагнетиков, вместо рассмотрения кулоновского взаимодействия электронных оболочек и связанного с ним обменного интеграла рассматривают обменное магнитное поле 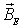, часто называемое молекулярным полем или полем Вейса, которое обеспечивает упорядоченное расположение магнитных моментов. Можно оценить величину этого поля. Согласно этим моделям, обменное магнитное поле создается системой упорядоченно расположенных магнитных моментов и оно же обеспечивает их упорядоченное расположение. Забегая вперед отметим, что поле Вейса имеет величину на 1-2 порядка большую наблюдаемых макроскопических полей, что в принципе считают возможным в отдельных точках кристалла.

Самым простой из упомянутых выше моделей описания ферромагнетиков является модель среднего поля, в основе которой лежит предположение, что на каждый магнитный момент действует магнитное поле 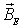пропорциональное намагниченности вещества:

 

.

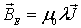(5.2)

Здесь 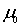- магнитная проницаемость вакуума.

Можно найти связь между параметрами и 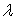. Для этого запишем связь между внешним полем 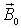относительной магнитной восприимчивостью 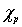и величинами 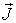, , 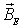известную из электродинамики:

 

.

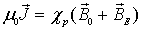(5.3)

В случае температур значительно превышающих 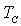можно использовать закон Кюри, известный из теории парамагнетизма:

 

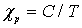
(5.4)

Подставив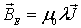

 и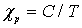

 в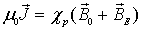

 и выразив из получившегося уравнения величину 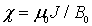, получим:

 

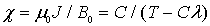
(5.5)

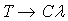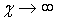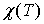Видно, что, если , то , что соответствует конечной намагниченности при внешнем поле . Именно такая картина наблюдается в случае ферромагнетика при . Отсюда заключают, что ; зависимость тогда имеет вид:

 

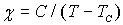
(5.6)

Это - сравнительно хорошо подтвержденный экспериментально закон Кюри-Вейса. На опыте наблюдаются незначительные отклонения от этого закона, в частности 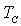в

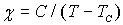
 оказывается на несколько градусов выше, чем , определенная по факту исчезновения спонтанной намагниченности ферромагнетика. Это объясняют тем, что при 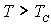сохраняется некоторый ближний порядок в расположении магнитных моментов, на расстояниях порядка нескольких межатомных. Тогда парамагнитное состояние вещества вблизи можно рассматривать как ферромагнитное с упорядоченным расположением магнитных моментов в очень малых областях и с большими значениями .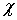

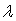Если использовать известное в теории парамагнетизма выражение для постоянной Кюри (см. том 3, 5), то для получается выражение:

 

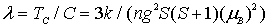
(5.7)

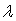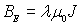Оценка величин и для случая железа, для которого 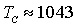К, фактор Ланде , дает и Тл. Значение 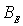оказывается очень большим, оно на несколько порядков превосходит наблюдаемые в кристаллах средние поля 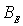, что показывает на нереалистичность объяснения магнитного упорядочения как результат чисто магнитного взаимодействия атомов. Тем не менее, такой подход в теории ферромагнетизма часто используется при вычислении температурной зависимости намагниченности.

Намагниченность при температурах ниже . Вычислим зависимость спонтанной намагниченности от температуры при 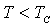. Для простоты рассмотрим случай, когда . Тогда, согласно теории парамагнетизма, зависимость 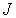от и 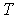имеет вид:

 

(5.8)

Если 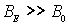, то , и выражение для примет вид:

 

(5.9)

Это уравнение относительно 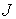можно решить только численными методами или графически (см. рис. 5.5), обозначив 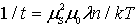и 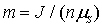. Оно имеет ненулевое решение при 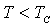. Результаты решения представлены на рис. 5.6.

Рис. 5.5. Графическое решение уравнения . Кривые 1 и 2 пересекаются в точке (0;0), а при 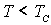и в темной точке вверху рисунка, соответствующей существованию ненулевой намагниченности при отсутствии внешнего поля .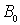

 

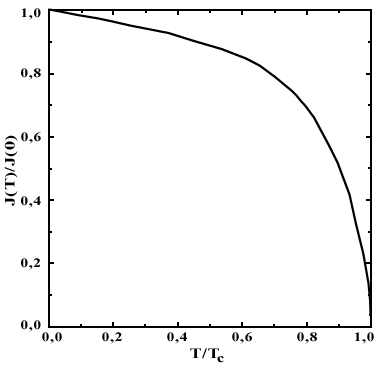
Рис. 5.6. Зависимость J(T), полученная как результат графического решения уравнения .

Можно показать (см. задачу 5.2), что при температуре 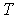меньшей и вблизи 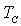зависимость 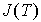имеет вид:

 

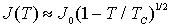
(5.10)

Примерно такая (с показателем степени не 1/2, а приблизительно 0,33) зависимость 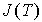наблюдается экспериментально для большинства ферромагнетиков. Отсутствие резкого скачка 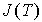вблизи дает основания отнести превращение ферромагнетика в парамагнетик при 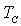к фазовому переходу второго рода.

Оценим ход зависимости 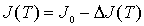вблизи абсолютного нуля. Для этого преобразуем

, воспользовавшись асимптотической формулой .

 

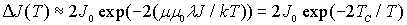
(5.11)

Эксперименты показывают другой характер изменения 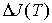при 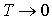, а именно:

 

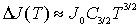
(5.12)

Постоянные 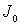и оказываются различными для разных ферромагнетиков.

Таким образом, теория среднего поля удовлетворительно описывает поведение намагниченности ферромагнетиков вблизи температуры Кюри, но дает крайне грубое описание 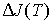при 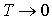. Теория спиновых волн, изложенная в [7], позволяет объяснить получаемую экспериментально степенную зависимость 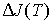. Мы рассмотрим в следующем разделе лишь основные выводы этой весьма сложной теории для случая ферромагнетиков.