Спиновые волны и магнитный вклад в теплоемкость

Спиновые волны. Теория спиновых волн рассматривает поведение магнитных моментов атомов (далее просто спинов, поскольку именно спиновый, а не орбитальный момент количества движения электронов обеспечивает наибольший вклад в свойства ферромагнетика) при низких температурах, когда ферромагнетик находится в основном состоянии, когда все спины параллельны друг другу. Для простоты рассматривают "линейную" цепочку из 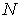спинов (см. рис. 5.7 а), каждый спин имеет спиновый момент 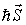; считают, что в цепочке взаимодействуют только ближайшие соседи. Энергию взаимодействия спинов в такой цепочке можно записать следующим образом:

(5.13)

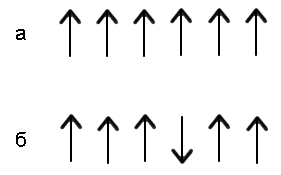
Через 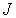здесь традиционно обозначают обменный интеграл. Тепловое движение при низких температурах может вносить "возбуждения" в эту систему, например, может переориентировать один из спинов в противоположную сторону (см. рис. 5.7 б).

Рис. 5.7. Ориентация спинов в линейной цепочке атомов: все спины сонаправлены (а), один спин в результате теплового движения приобрел противоположную ориентацию (б).

При этом две пары спинов будут противоположно направлены, и система спинов из-за этого приобретет дополнительную энергию:

(5.14)

Эта энергия - сравнительно велика (см. разд. 5.4), меньшей энергии соответствуют возбуждения системы спинов, схематически изображенные на рис. 5.8. В этом случае при переходе от спина к спину происходит незначительная ориентация каждого спина, а само распределение ориентаций спинов напоминает волну. Поэтому такие возбуждения спиновой системы принято называть спиновыми волнами. Эти возбуждения квантуются, квант принято называть магноном и рассматривать как квантовую квазичастицу, подобно тому, как рассматривали фононы и фотоны в главе 3 этой книги и в томе 5 данного курса. Можно показать, что каждый магнон уменьшает 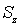-компоненту общего спина на единицу.

Рис. 5.8. Ориентация спинов в линейной цепочке атомов в случае спиновой волны: все спины почти сонаправлены. Распределение ориентировок спинов напоминает волну

Можно вывести (см. [7]) закон дисперсии 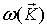для магнонов, возбуждаемых в рассмотренной цепочке или в реальной структуре. Например, для линейной цепочки (см. рис. 5.7) получается закон дисперсии:

(5.15)

Для кубических решеток можно аналогичным образом получить закон дисперсии:

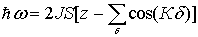
(5.16)

Суммирование в 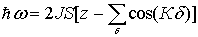 проводят по всем векторам, соединяющим выбранный узел решетки со всеми ближайшими соседями.

Общим для этих случаев является зависимость при малых .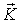

(5.17)

Зависимость энергии (или частоты 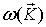) магнонов от их волнового вектора 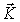может быть определена с помощью рассеяния нейтронов в точности по той же схеме, как это делается для фононов (см. разд. 3.1). На рисунке 5.9 приведена зависимость 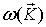для кобальта и для сравнения рассчитанная по формуле

. Видно, что в случае малых энергия магнона почти не зависит от направления вектора , как и предсказывает теория спиновых волн.

Рис. 5.9. Зависимость 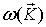для кобальта для различных направлений вектора 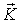по направлениям [100], [110], [111].

Можно показать, что энергия магнонов 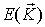вычисляется по тем же формулам, что и для фотонов и фононов: как . Магноны рассматривают как бозоны и применяют к ним формулы статистики Бозе-Эйнштейна, как это делалось в главе 3 этой книги, с тем лишь отличием, что закон дисперсии для магнонов другой - он дается формулами (5.15-5.17), а не формулами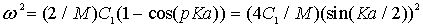

, справедливыми для фононов. Также отметим, что магноны имеют одну поляризацию (а не три поляризации - как фононы или две - как фотоны в вакууме).

По той же самой схеме как это делалось в разделе 3.3 можно рассчитать вклад магнонов во внутреннюю энергию и в теплоемкость ферромагнетика (см. задачу 5.4). Эти вычисления показывают, что магнитный вклад в теплоемкость при низких температурах пропорционален , что соответствует экспериментальным данным.

Примерно по той же схеме вычисляют 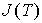и 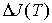при низких температурах. При этом учитывают, что каждый магнон, согласно [7], уменьшает магнитный момент ферромагнетика на одну и ту же величину. В таком случае 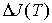оказывается пропорциональной общему числу магнонов в единице объема ферромагнетика при заданной температуре, которая легко вычисляется с помощью распределения Бозе-Эйнштейна. Можно показать (см. задачу 5.3), что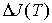 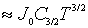. Здесь 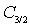- константа, зависящая от структуры ферромагнетика.

Вклад в теплоемкость ферромагнетиков вблизи 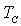. Для многих ферромагнетиков магнитный вклад в теплоемкость сопоставим с вкладом обусловленным колебаниями кристаллической решетки, а вблизи значительно превосходит его. На рис. 5.10 приведена температурная зависимость различных вкладов в молярную теплоемкость никеля при различных температурах.

Рис. 5.10. Температурная зависимость различных вкладов в молярную теплоемкость никеля при различных температурах Т

Видно, что вблизи температуры Кюри зависимость 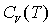имеет максимум похожий на "зуб" вблизи 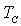. На этом основан часто используемый метод определения 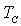по экспериментально измеренной зависимости 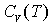. Метод особо полезен для случая многофазных материалов с фазами неизвестного состава, тогда по фаз можно получать сведения о составе этих фаз. Этот метод определения температуры разрушения доменной структуры применим и для случаев как антиферромагнетиков, так и ферримагнетиков и веществ с более сложной картиной упорядочения спинов.