Любые атомы можно характеризовать единым механическим моментом 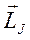 и единым магнитным моментом
и единым магнитным моментом 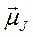 , которые являются результирующими сложения орбитальных и спиновых моментов всех электронов и ядра. Моментами ядер можно пренебречь.
, которые являются результирующими сложения орбитальных и спиновых моментов всех электронов и ядра. Моментами ядер можно пренебречь.
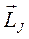 и
и 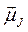 атома должны быть квантованы в соответствии с общими правилами квантования,
атома должны быть квантованы в соответствии с общими правилами квантования,
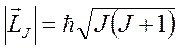 ;
; 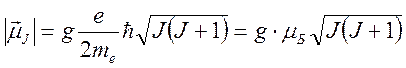 ,
,
где 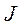 - полное (или внутреннее) квантовое число атома.
- полное (или внутреннее) квантовое число атома.
Полный механический момент атома (системы)
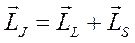 или
или 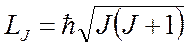
Наложение условия квантования механического момента приводит к двум различным возможностям геометрического сложения моментов, которые можно свести к алгебраическому сложению квантовых чисел.
1) Если отдельные орбитальные моменты электронов в атоме взаимодействуют между собой сильнее, чем орбитальные и спиновые моменты для отдельных электронов, то вначале надо векторно складывать орбитальные моменты всех электронов атома, а затем – спиновые моменты электронов и только потом складывать их между собой:
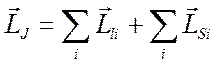 .
.
Такая связь между механическими моментами называется связью Рессель-Саундерса.
2) Если сильнее взаимодействуют орбитальные и спиновые моменты отдельных электронов между собой, то следует находить результирующий момент для каждого электрона, а затем складывать эти моменты между собой:
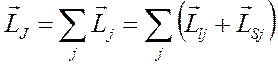 .
.
Такой вид связи называется « » связью.
» связью.
Рассмотрим связь Рессель-Саундерса
Суммарный орбитальный момент системы (атома)
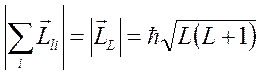 ,
,
где 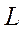 - орбитальное квантовое число атома.
- орбитальное квантовое число атома.
Если атом состоит из 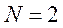 электронов, то
электронов, то  . Квантовое число
. Квантовое число 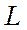 может иметь
может иметь 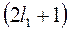 или
или 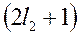 значений (надо взять меньшее из них). Например, для
значений (надо взять меньшее из них). Например, для 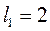 , а
, а 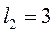 получаем
получаем 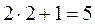 значений, т.е.
значений, т.е.  . Если
. Если 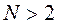 , то
, то 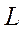 определяется последовательным применением правила
определяется последовательным применением правила
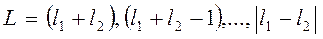 .
.
Проекция орбитального момента на ось 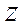
 ,
,
где 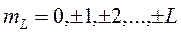 .
.
Суммарный спиновый момент системы
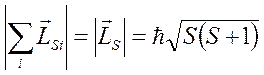 ,
,
где 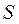 - квантовое число результирующего спинового момента, оно может быть целым или полуцелым. Если число электронов в атоме
- квантовое число результирующего спинового момента, оно может быть целым или полуцелым. Если число электронов в атоме  - четное, то
- четное, то 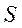 вычисляется по правилу
вычисляется по правилу 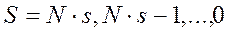 , где
, где 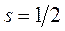 и число
и число  будет принимать целые значения. Например,
будет принимать целые значения. Например,  , тогда
, тогда 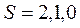 . Если
. Если  - нечетное, то
- нечетное, то 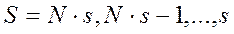 - принимает полуцелые значения. Например, при
- принимает полуцелые значения. Например, при 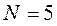
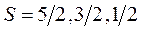 .
.
Единый механический момент атома
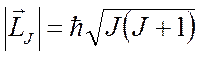
определяется полным квантовым числом системы, которое может принимать значения
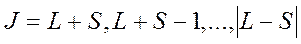 .
.
Отсюда следует, что геометрическое сложение моментов можно свести к алгебраическому сложению квантовых чисел.
Пусть один электрон находится в состоянии с  , а другой - с
, а другой - с 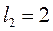 . Орбитальные моменты этих электронов соответственно равны:
. Орбитальные моменты этих электронов соответственно равны:
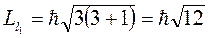 ;
; 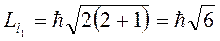 .
.
 |
Суммарный орбитальный момент системы может принимать различные значения в зависимости от взаимной ориентации 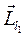 и
и 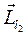 . Орбитальное квантовое число
. Орбитальное квантовое число 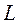 может принимать значения
может принимать значения 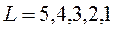 . Значит, возможны пять значений результирующего орбитального момента, максимальное из которых, соответствующее
. Значит, возможны пять значений результирующего орбитального момента, максимальное из которых, соответствующее 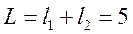 , будет при
, будет при 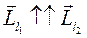
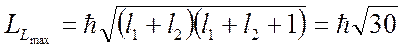 ,
,
а максимальная проекция результирующего момента
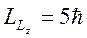 .
.
Минимальное значение - при 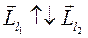
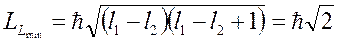
соответствует наименьшему числу 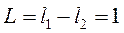 . И минимальная проекция на ось
. И минимальная проекция на ось  будет
будет 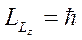 .
.
Два момента не могут быть строго параллельными или антипараллельными друг другу.
Для системы из двух валентных электронов 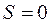 или
или 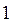 При
При 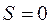 спиновый механический момент атома
спиновый механический момент атома 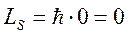 и результирующий момент атома совпадает с результирующим орбитальным моментом (
и результирующий момент атома совпадает с результирующим орбитальным моментом (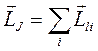 ). Поскольку
). Поскольку 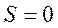 , то мультиплетность спектра будет отсутствовать (мультиплетность равна
, то мультиплетность спектра будет отсутствовать (мультиплетность равна  ), т.е. термы, соответствующие этим состояниям, будут одиночными (синглетными).
), т.е. термы, соответствующие этим состояниям, будут одиночными (синглетными).
При  результирующий спиновый момент атома
результирующий спиновый момент атома
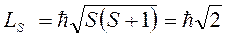 .
.
Тогда полное квантовое число атома будет 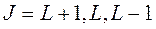 , где
, где 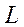 - суммарное орбитальное квантовое число, т.е. реализуется три квантовых числа в зависимости от взаимной ориентации орбитальных и спиновых моментов. Мультиплетность в этом случае равна 3 (триплет).
- суммарное орбитальное квантовое число, т.е. реализуется три квантовых числа в зависимости от взаимной ориентации орбитальных и спиновых моментов. Мультиплетность в этом случае равна 3 (триплет).
Соответствующие состояния принято записывать так:
(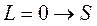 ;
; 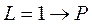 ;
; 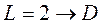 ;
; 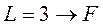 и т.д.),
и т.д.),
справа внизу ставится полное квантовое число 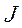 , а слева вверху – мультиплетность (
, а слева вверху – мультиплетность (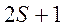 ). Например,
). Например, 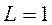 ,
, 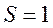 ,
,  :
: 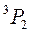 ,
, 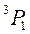 ,
, 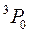 .
.
Если при 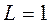 будет
будет 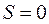 , то
, то 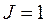 и терм синглетного состояния
и терм синглетного состояния 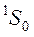 .
.
Если число валентных электронов четно, то 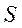 равно нулю или целому числу - мультиплетность термов будет нечетной. Если количество валентных электронов в атоме нечетно, то
равно нулю или целому числу - мультиплетность термов будет нечетной. Если количество валентных электронов в атоме нечетно, то 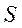 будет полуцелым и мультиплетность будет четной.
будет полуцелым и мультиплетность будет четной.
При переходе электронов между термами действуют следующие правила отбора: 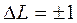 ,
, 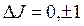 .
.
 2020-10-12
2020-10-12 233
233







