Декартовы координаты в пространстве

Совершенно аналогично вводятся координаты в пространстве. А именно, берутся три координатные оси, пересекающиеся в одной точке и не лежащие в одной плоскости. Масштабные единицы на осях, вообще говоря, могут быть опять вы­браны различные. Кроме них, для из­мерения всех длин в пространстве выбирается общая «абсолютная масштабная единица», которой, в частности, измеряются и длины масштабных единиц на осях. В качестве начала отсчета на всех трех осях берется точка их пересечения О (начало координат). Одну из координатных осей называют осью абсцисс (осью х), другую — осью ординат (осью у) и третью — осью аппликат (осью z). Плоскость, проходящая через оси х и у, называется координатной плоскостью ху, плоскость, проходящая через оси у и z,—координатной плоскостью уz и плоскость, проходящая через оси х и z, — координатной плоскостью хz. Для того чтобы задать числами положение точки М в пространстве, проводят через эту точку плоскости, параллельные координатным плоскостям. Плоскость, параллельная координатной плоскости уz, пересечет ось абсцисс в некоторой точке М 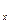; плоскость, параллельная координатной плоскости xz, пересечет ось ординат в некоторой точке М 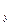; плоскость, параллель­ная координатной плоскости ху, пересечет ось аппликат в некоторой точке М 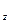. Пусть х, у, z— координаты точек 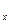М 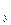, М , М 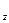 на соответствующих осях. Положение точки М вполне определяется заданием чисел х, у, z. Эти числа называются декартовыми коор­динатами точки М, при этом х — абсциссой, у — ординатой и z — аппликатой. Параллелепипед O 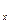М 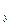 М  М 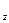ABCM, высекаемый координатными плоскостями и параллельными им плоскостями, проходящими через точку М, называется координатным параллелепипедом точки М; его ребра (и в частности от­резки О 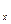М 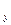, М , М 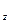) называются координатными отрезками точки М. Чтобы указать, что точка М имеет координаты х, у и z, пишут: M{x,y,z); при этом абсциссу поме­щают на первом месте, ординату — на втором и аппликату — на третьем. Точку с абсциссой х, ординатой у и аппликатой z записывают также символом (х,у, z). Таким образом, каждой точке пространства соответствует вполне определенная упорядоченная тройка вещественных чисел; обратно, каждой упорядочен­ной тройке вещественных чисел соответствует вполне определен­ная точка пространства. Иными словами, между совокупностью всех точек пространства и совокупностью всех упорядоченных троек вещественных чисел установлено взаимно однозначное соответствие. Начало координат О имеет координаты 0, 0, 0. Точки оси абсцисс имеют вид (х, 0, 0), точки оси ординат—вид(0, у, 0), точки оси аппликат — вид (0,0, z). Точки координатной плоскости ху имеют вид (х, у, 0), точки координатной плоскости yz — вид (0, у, z), точки координатной плоскости xz — вид (х, 0, z). Коорди­натные плоскости разбивают все пространство на восемь трехгран­ных углов.

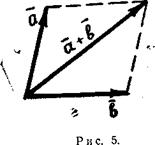
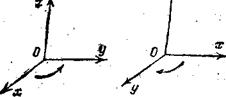5. Правая и левая системы координат в пространстве. На рис. изображены два типа взаимного расположения координатных осей в пространстве. Представим себя в роли наблюдателя, стоящего на плоскости ху с той ее стороны, в которую обращена ось z, и обращенного в сторону положительного направления оси х. Тогда в случае, изображенном на черт.1, ось у будет, идти справа налево и система координат на плоскости ху будет представляться нам как правая, а в случае, изображенном на черт, 2, ось у будет идти слева направо и система координат на плоскости ху будет представляться нам как левая. В первом случае координатную систему хуz называют правой, во втором — левой.

В случае плоскости обычно пользуются правой системой координат; при этом ocь х чертят горизонтально и поло­жительным направлением на ней считают направление слева на­право; тогда положительным направлением на оси у является направление снизу вверх. В случае пространства пользуются и той и другой системой координат; мы будем пользоваться преимущественно правой.

6. Общие декартовы; косоугольные и прямоугольные коорди­наты. Описанные координаты — как на плоскости, так и в пространстве — называются общими декартовыми координатами. Если масштабные единицы на осях совпадают с выбранной абсолютной масштабной единицей, но углы между осями — не все прямые, то получаем так называемые косоугольные координаты, которыми много пользовались в некоторых прежних курсах аналитической геометрии; мы ими пользоваться совсем не будем. Если, кроме того оси взять взаимно перпендикулярными, то получатся прямоугольные координаты, наиболее часто употребляемые в практике.

Таким образом, прямоугольными координатами называются декар­товы координаты, удовлетворяющие двум условиям: 1) координатные оси взаимно перпендикулярны и 2) масштабные единицы на осях совпадают с абсолютной единицей измерения длин. В наимено­вании этих координат прямоугольными отражено только первое из этих двух условий.

Сложение векторов

Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника

Правило треугольника. Для сложения двух векторов 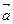 и 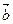 по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора.

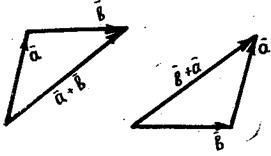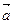Пусть  и 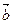 — два произвольных вектора. Приложим век­тор  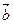к концу вектора 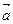, то есть совместим начало вектора  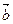с концом вектора 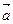. Тогда вектор, идущий из начала векто­ра  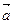в конец вектора  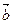называется суммой векторов  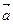и 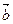 и обозначается  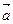+ 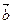. Такой способ построения суммы двух век­торов  называют «правилом треугольника» (рис.).

Если начало вектора 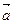 совместить с концом вектора  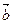(рис.), то вектор, идущий из начала вектора  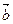в конец век­тора 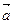, будет вектором суммы  + .

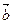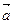Чтобы получить вектор суммы 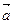 +  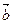можно воспользо­ваться также «правилом параллелограмма». Для сложения двух векторов  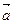и 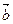по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.

 Как видно, сумма двух векторов обладает переместительным свойством, то есть  +  =  + .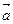

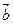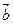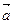Понятие суммы двух векторов можно обобщить на случай любого конечного числа слагаемых. Пусть, например, даны три вектора 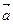,  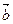и с и требуется найти их сумму  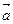+  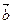+ с. Искомый вектор можно получить, последовательно применяя правило треугольника:

прикладываем вектор 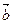 к вектору  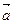и получаем вектор  + ;                   

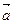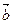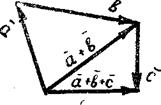
вектор (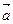 + 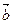) складываем с вектором 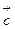и получаем искомый вектор  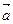+  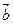+  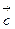(рис.5).

Из рис.  видно, что искомый вектор суммы трех векторов можно получить, если к вектору 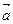 приложить вектор 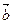, к век­тору  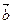приложить вектор 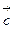и тогда вектор, идущий от начала первого вектора до конца последнего вектора будет искомым.

Это правило, называемое «правилом многоугольника», остается справедливым при нахождении суммы любого конеч­ного числа векторов. При этом сумма не зависит от порядка слагаемых.

Если при сложении нескольких векторов конец последнего вектора совпадает с началом первого вектора, то сумма рав­на нуль-вектору.

? Какой особенностью отличается многоугольник векторов, сумма которых равна нулю?

Вычитание векторов

Если даны два вектора 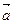 и 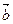, то разностью  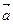—  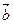назы­вается такой третий вектор с, который в сумме с вектором  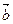составляет вектор .

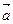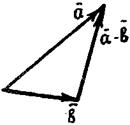Из определения суммы двух векторов вытекает правило построения вектора разности: векторы  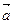и 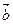 приводят к об­щему началу и тогда вектор, идущий от конца вектора  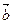к концу вектора 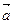, будет искомым (рис.).

Вычесть из вектора 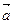 вектор  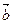означает, что к вектору  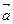надо прибавить вектор — 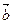, то есть  —  =  + (— ).

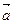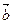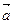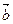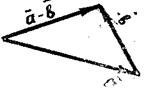На рис. к вектору  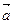приложен вектор —  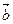и, пользуясь правилом треугольника, найдена разность  — .

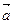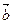Способ замены вычитания сложением удобен тогда, когда требуется построить алгебраическую сумму нескольких век­торов.