ЛЕКЦІЯ 3. ВЕКТОРНА АЛГЕБРА
1. Вектори. Операції над ними.
Вектором називається спрямований відрізок. Вектор з початком в точці 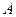 і кінцем у точці
і кінцем у точці 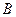 позначається символом
позначається символом 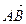 (або однією буквою
(або однією буквою 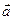 ,
, 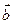 ,...).
,...).
Модулем (довжиною) вектора 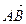 називається довжина відрізка
називається довжина відрізка 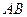 і позначається,
і позначається, 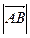 ,
, 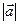 .
.
Одиничним називається вектор, довжина якого дорівнює одиниці. Одиничний вектор позначають 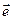 .
.
Нульовим називається вектор, довжина якого дорівнює нулю. Нульовий вектор позначається 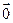 .
.
Колінеарними називаються вектори 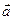 і
і 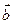 , якщо вони лежать на одній прямій або на паралельних прямих; записують
, якщо вони лежать на одній прямій або на паралельних прямих; записують 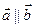 .
.
Компланарними називаються три (і більше) вектора, якщо вони лежать в одній площині або в паралельних площинах.
Рівними називаються два колінеарних вектори 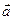 и
и 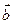 (
(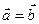 ), якщо вони однаково спрямовані і мають рівні довжини.
), якщо вони однаково спрямовані і мають рівні довжини.
Додавання векторів.
Сумою двох векторів 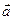 і
і 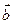 називається вектор
називається вектор 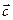 , що з'єднує початок вектора
, що з'єднує початок вектора 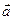 з кінцем вектора
з кінцем вектора 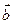 , відкладеного від кінця вектора
, відкладеного від кінця вектора 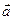 .
.
.
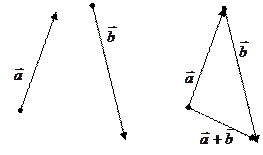
Добуток вектора на число.
Добутком вектора 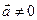 на число
на число 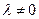 називається вектор, який має довжину
називається вектор, який має довжину 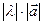 і який має напрям вектора
і який має напрям вектора 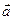 в разі
в разі 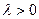 та протилежний напрямок у разі
та протилежний напрямок у разі 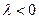 .
.
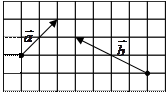
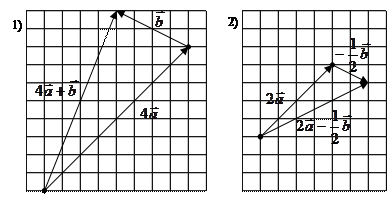
Приклад.1. Дано вектори 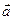 і
і 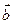 . Побудуйте вектори: 1) 1)
. Побудуйте вектори: 1) 1) 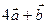 ; 2)
; 2) 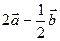 .
.
Декартові прямокутні координати вектора. Довжина вектора.
Нехай вектор 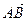 складає кут
складає кут 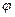 з віссю
з віссю 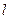 .
.
Проекцією вектора 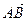 на вісь
на вісь 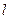 називається число, рівне довжині вектора
називається число, рівне довжині вектора 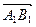 (рис.1), взятої зі знаком «плюс», якщо напрям вектора
(рис.1), взятої зі знаком «плюс», якщо напрям вектора 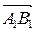 збігається з напрямком осі і зі знаком «мінус» у противному випадку.
збігається з напрямком осі і зі знаком «мінус» у противному випадку.
Проекцію вектора 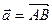 на вісь
на вісь 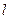 можна обчислити за формулою:
можна обчислити за формулою:
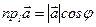 .
.
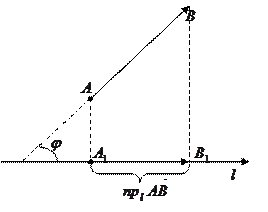
Декартовими прямокутними координатами 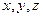 вектора
вектора 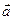 називаються його проекції на відповідні координатні осі
називаються його проекції на відповідні координатні осі 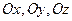 .
.
Вектор 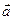 з координатами
з координатами 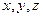 записують у вигляді
записують у вигляді 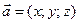 або,
або, 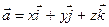 де
де 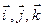 - одиничні вектори координатних осей
- одиничні вектори координатних осей 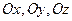 відповідно. Довжина вектора
відповідно. Довжина вектора 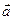 визначається за формулою:
визначається за формулою:
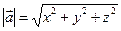 .
.
Якщо вектор 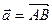 заданий точками
заданий точками 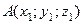 і
і 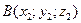 , то його координати обчислюються за формулами:
, то його координати обчислюються за формулами:
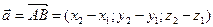 .
.
Приклад 2. Дано дві точки 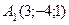 і
і 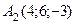 . Знайдіть координати і довжину вектора
. Знайдіть координати і довжину вектора 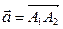 .
.
За умовою задачі, 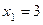 ,
, 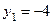 ,
, 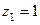 ,
, 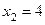 ,
,  ,
,  . Значить,
. Значить, 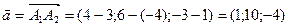 .
.
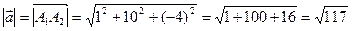 .
.
Приклад 3. Дано два вектори 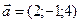 и
и 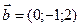 . Знайдіть координати і довжину вектора
. Знайдіть координати і довжину вектора 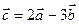 .
.
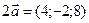 ;
; 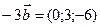 ;
;
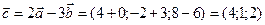 ;
;
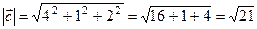 .
.
Поєднаємо паралельним переносом початок деякого вектора 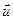 з початком координат прямокутної системи координат
з початком координат прямокутної системи координат 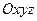 . Нехай
. Нехай 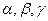 - кути, які утворює вектор
- кути, які утворює вектор 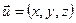 з осями координат
з осями координат 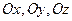 відповідно (рис.2). Напрям вектора
відповідно (рис.2). Напрям вектора 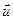 визначається за допомогою направляючих косинусів
визначається за допомогою направляючих косинусів 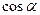 ,
, 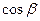 ,
, 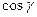 , для яких справедливі рівності:
, для яких справедливі рівності:
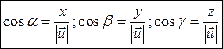 , ,
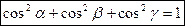 . .
| 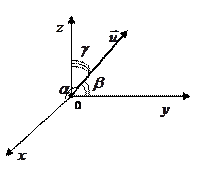
|
3. Скалярний добуток векторів.
Скалярним добутком двох ненульових векторів 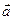 і
і 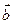 називається число, рівне добутку довжин цих векторів на косинус кута
називається число, рівне добутку довжин цих векторів на косинус кута 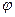 між ними (див. рис.3):
між ними (див. рис.3):
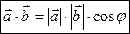 .
.
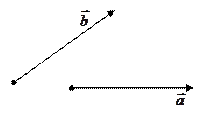
| 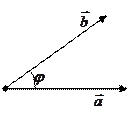
|
З рис. 3 видно, що 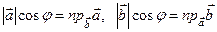 .
.
Тому 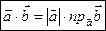 або
або 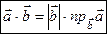 . (*)
. (*)
 2020-10-12
2020-10-12 111
111







