Прямые методы вариационного исчисления

Конечно-разностный метод Эйлера

Пусть дана простейшая вариационная задача: найти экстремум функционала

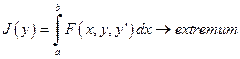                         (8)

с заданными граничными условиями:

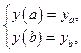                                                 (9)

где F (x, y, y ¢) — непрерывная функция трёх переменных и дифференцируемая функция двух своих последних аргументов.

Решаем задачу методом Эйлера – значения функционала (8) рассматриваются не на произвольных, допустимых в данной вариационной задаче кривых, а лишь на ломаных, составленных из заданного числа N прямолинейных звеньев, с заданными абсциссами вершин

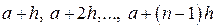, где .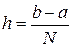

На этих ломаных функционал (8) превращается в функцию 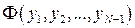 ординат  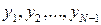вершин ломаной. Ординаты  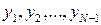выбираются так, чтобы функция  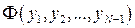достигала экстремума, т. е. они определяются из системы уравнений

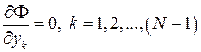
(ординаты 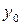 и 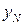 известны из граничных условий ).

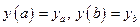Метод Ритца

Метод Ритца представляет собой один из методов построения минимизирующей последовательности для функционала.

Решение уравнения

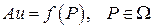,                                       (6)

где А — положительный оператор, сводится к нахождению минимума функционала

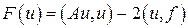,                                (7)

где скалярное произведение

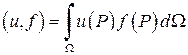.                                (8)

Эту последнюю задачу будем приближенно решать следующим образом. Выберем последовательность

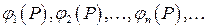     ,                           (9)

координатных функций, принадлежащих области определения оператора D_A; подчиним эту последовательность двум условиям:

1. последовательность (9) полна по энергии;

2. при любом n функции 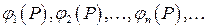  линейно независимы.

Построим линейную комбинацию первых n координатных функций

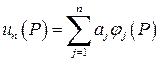                                          (10)

с произвольными численными коэффициентами a_j. Подставим u_n (P) вместо u (P) в функционал (7); это превратит F (u) в функцию n независимых переменных a₁, a₂, …, a_n:

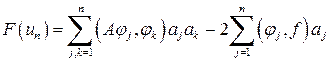    .            (11)

Выберем коэффициенты a_j так, чтобы функция (11) приняла минимальное значение. Функция (11) достигает минимума при тех значениях независимых переменных, которые обращают в нуль ее первые производные:

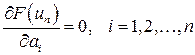    .                              (12)

Уравнения (12) дают, как известно, необходимые условия минимума F(u_n). Однако, используя положительность оператора A, можно доказать, что коэффициенты a_j, удовлетворяющие системе (12), реализуют минимум величины F (u_n).

Соотношения (12) представляют собой систему линейных алгебраических уравнений

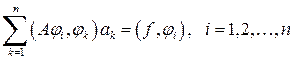    .           (13)

Определитель системы (13) есть определитель Грамма линейно независимых функций и потому отличен от нуля. Отсюда следует, что система уравнений Ритца всегда разрешима, если оператор А — положительный.

Найдя коэффициенты a₁, a₂, …, a_n и подставив их в (10), получим функцию u_n (P), которую будем называть приближенным решением уравнения (6) по Ритцу.