Пользуясь методом Ритца, найти экстремали функционала
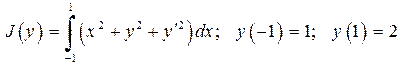 .
.
Показать сходимость полученного приближенного решения к точному при возрастании числа элементов, используемых в аппроксимации. Построить графики решений.
Решение. Будем решать задачу в среде Maple. Определяем подынтегральную функцию:
> restart;
> F:=(x,y,y1)->x^2+y^2+y1^2;

Составим уравнение Эйлера для данного функционала. Для этого вычислим частные производные от F по y и y1 и полную производную по x от частной производной F по y1 (переменная y1 означает первую производную, а переменная y2 – вторую производную)
> dFdy:=diff(F(x,y,y1),y);dFdy1:=diff(F(x,y,y1),y1);
> d_dFdy1_dx:=diff(dFdy1,x);d_dFdy1_dy:=diff(dFdy1,y);
> d_Fdy1_dy1:=diff(dFdy1,y1);


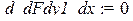
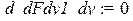
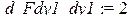
Составим теперь уравнение Эйлера
> eq:=dFdy-d_dFdy1_dx-d_dFdy1_dy*y1-d_Fdy1_dy1*y2=0;

> eq:=simplify(lhs(eq)/2)=0;
> eq:=subs(y=y(x),y2=diff(y(x),x$2),lhs(eq))=0;


Решим полученное уравнение с заданными граничными условиями
> res:=dsolve({eq,y(-1)=1,y(1)=2},y(x));
> assign(res):y:=evalf(y(x));
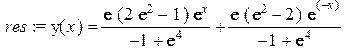
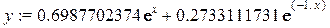
Построим график точного решения
> py:=plot(y,x=-1..1,legend=`Точное решение`,
color=black):
> plots[display]({py});

Решим теперь эту задачу с помощью пакета VariationalCalculus:
> with(VariationalCalculus);

Определяем подынтегральную функцию:
> y:='y':f:=x^2+y(x)^2+diff(y(x),x)^2;
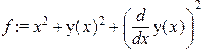
> EulerLagrange(f, x, y(x));

Решим уравнение Эйлера с заданными граничными условиями
> res1:=dsolve({op(%)=0,y(-)=1,y(1)=2},y(x));
assign(res1):y:=evalf(y(x));
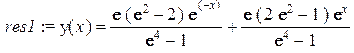

То есть, как и следовало ожидать, получили тот же результат!
Решаем теперь нашу задачу методом Ритца. Выбираем базисные функции и определяем аппроксимирующую функцию. Рассмотрим два варианта — аппроксимация полиномами и аппроксимация тригонометрическими функциями:
> phi0:=x->y1+(y2-y1)*(x-x1)/(x2-x1);
> phi:=(x,n)->sin(n*Pi*(x-x1)/(x2-x1));
> Us:=proc(x,N)option operator,arrow; local n;
phi0(x)+sum(a[n]*phi(x,n),'n'=1..N);
end proc;
> Up:=proc(x,N)option operator,arrow; local n;
phi0(x)+(x-x1)*(x-x2)*sum(a[n]*x^n,'n'=0..N);
end proc;

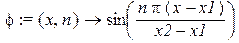
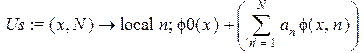

С целью автоматизации расчетов разработаем процедуру, формирующую и решающую систему уравнений метода Ритца, например, такую
> Ritz:=proc(F,u,i0,N,a)
local Fu,eqns,var,eq,i,res;global x1,x2;
Fu:=simplify(int(subs(y(x)=u,F),x=x1..x2)):
eqns:={}:var:={}:
for i from i0 to N do
var:=var union {a[i]}:
eq[i]:=diff(Fu,a[i])=0:
eqns:=eqns union {eq[i]}:
od:
res:=solve(eqns,var);
assign(res);
end proc:
Определим теперь нашу подынтегральную функцию
> F:=x^2+y(x)^2+diff(y(x),x)^2;

Зададим граничные точки
> x1:=-1;x2:=1;y1:=1;y2:=2;


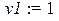
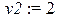
Задаемся числом аппроксимирующих функций и решаем задачу
> N:=3:c1:=`cross`:c2:=`circle`:c3:=`box`:
> for j from 1 to N do
a:=array(1..j):u:=Us(x,j):
Ritz(F,u,1,j,a);
pUs_||j:=
plot(Us(x,j),x=-1..1,
color=black,style=point,symbol=c||j,
legend=cat(`Метод Ритца N = `,convert(j,string))):
end do:

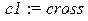
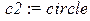
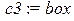
Отображаем решение на графиках
> plots[display]({pUs_1,pUs_2,pUs_3,py});

Видим, что удержание трех членов ряда вполне достаточно. Покажем эти аппроксимации
> Us(x,1);Us(x,2);Us(x,3);
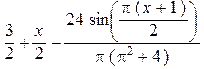
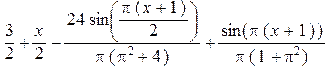
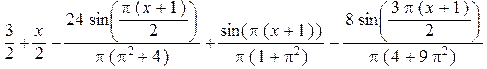
Рассмотрим теперь решение задачи с помощью аппроксимации полиномами
> N:=2:c1:=`cross`:c2:=`circle`:
> c3:=`box`:c0:=`diamond`:
> for j from 0 to N do
a:=array(0..j):u:=Up(x,j):
Ritz(F,u,0,j,a);
pUp_||j:=
plot(Up(x,j),x=-1..1,color=black,
style=point,symbol=c||j,
legend=cat(`Метод Ритца N = `,convert(j,string))):
end do:

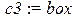

Отобразим решение на графиках
> plots[display]({pUp_0,pUp_1,pUp_2,py});

Видим, что и в этом случае удержание трех членов ряда вполне достаточно. Покажем полученные аппроксимации
> Up(x,0);Up(x,1);Up(x,2);
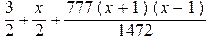


 2020-10-12
2020-10-12 189
189








