Математическая модель и особенности транспортной задачи

РАСПРЕДЕЛИТЕЛЬНЫЙ МЕТОД

ТЕМА 4

Распределительный метод широко применяется при решении главным образом различных транспортных задач (оптимальное закрепление потребителей груза за поставщиками, маршрутизация перевозок грузов, распределение парка подвижного состава по АТП, закрепление маршрутов за АТП и др.), поэтому его иногда называют транспортным методом.

Прежде чем перейти к изложению алгоритма метода, познакомимся с моделью и особенностями классической транспортной задачи (такое название получила задача нахождения оптимальных грузопотоков, т. е. оптимального закрепления поставщиков однородного груза за потребителями).

Модель транспортной задачи в общем виде записывается в следующей форме:

где і — количество поставщиков; ј — количество потребителей; а_і — ограничения по предложению; b_j — ограничения по спросу; с_іј — элементы целевой матрицы; х_іј — объем корреспонденции между і- й и j -й точками.

Критерием оптимальности в транспортной задаче может быть минимум грузовой работы в тонно-километрах, затраты времени или стоимость перевозки.

Рассмотрим конкретный пример транспортной задачи.

Пусть имеются три грузообразующих точки А₁ А₂ и А₃, из которых следует вывезти однородный груз четырем потребителям (В₁, В₂, В₃, В₄) в количестве соответственно 400, 600 и 1000 т. При этом потребителю В₁ необходимо доставить 200 т. груза, В₂ — 400, В₃ — 800 и В₄—600т..

Расстояния между грузоотправителями и потребителями указаны в табл. 1.

Таблица 1

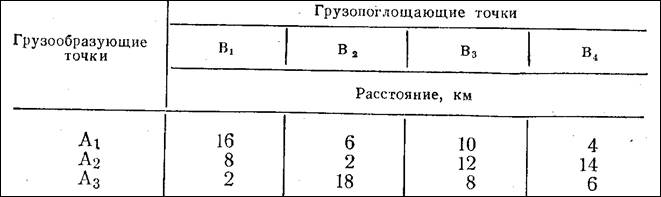
Необходимо так закрепить потребителей груза за грузоотправителями, чтобы общая транспортная работа была минимальной.

В этой задаче неизвестно количество груза, которое следует перевозить от каждого отправителя конкретному потребителю.

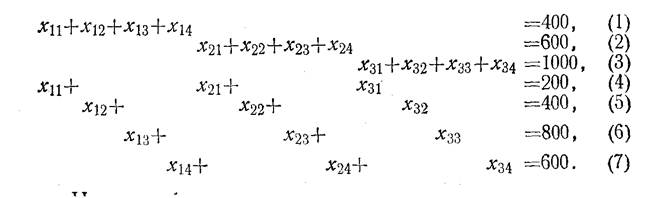
Обозначим через х_ij количество тонн груза, которое должно быть перевезено от i- го поставщика j -му потребителю. Тогда модель задачи выразится следующей системой уравнений:

Целевая функция будет представлять собой сумму произведений расстояний на соответствующий объем перевозок груза в тоннах:

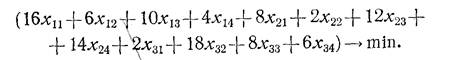Всe неизвестные могут принимать положительные значения или равняться нулю, т. е. хij ≥ 0.

Модель транспортной задачи имеет следующие особенности:

1. Выражается неопределенной системой линейных уравнений и, следовательно, имеет бесчисленное множество возможных решений.

2. Она совместна, т. е. имеет решение.

3. Элементами матрицы системы являются единицы и нули.

4. Система является линейно зависимой, так как любое ее уравнение можно представить в виде линейной комбинации остальных уравнений. Например, если из суммы уравнений (1), (2), (3) вычесть суммы уравнений (4), (5) и (6), то получим уравнение (7).

5. Число линейно независимых уравнений всегда на одно меньше общего количества уравнений в системе, так как без любого одного уравнения каждое оставшееся уравнение нельзя представить как линейную комбинацию из других уравнений. Следовательно, базис системы равен количеству уравнений за вычетом единицы. В нашем примере базис равен 6(7 - 1 = 6).

6. Целевая функция выражается линейной формой. Матрица целевой функции — это матрица-строка, элементами которой могут быть расстояния, время или стоимость перевозки.

Ввиду особенностей математической формы и постановки транспортной задачи линейного программирования «для решения ее разработаны специальные методы, позволяющие из бесчисленного множества возможных решений найти оптимальное. Одним из таких методов является распределительный, имеющий несколько разновидностей, которые отличаются в основном способом выявления оптимального решения.

2. Первый способ (метод Хичкока)

В табл. 2 записываются все исходные данные задачи. Расстояния между грузообразующими и грузопоглощающими точками заносятся в отчеркнутые правые углы клеток. Эта таблица называется матрицей распределительного метода.

Распределение груза по потребителям производится начиная с грузоотправителя А₁ и грузополучателя В₁ т. е. с клетки А₁В₁. Потребность в грузе потребителя В₁ удовлетворяется полностью грузоотправителем А₁. В клетку А₁В₁ табл. 2 записывается весь объем потребления грузополучателя В_І — 200 т. Оставшийся в точке А₁ груз в количестве 200 т будет вывозиться потребителю В₂. Но потребителю В₂ нужно завезти не 200, а 400 т груза. Недостающие 200 т груза можно возить от грузоотправителя А₂. Оставшиеся у грузоотправителя А₂ 400 т груза можно вывезти в точку В₃ и т. д. Рассуждая таким образом, распределим весь груз по потребителям.

В табл. 2 распределение груза по потребителям (закрепление потребителей за грузоотправителями) выразится в заполнении соответствующих клеток (А1В1 А_ІВ₂, А₂В₂; А₂В₃; А₃В₃; А₃В₄).

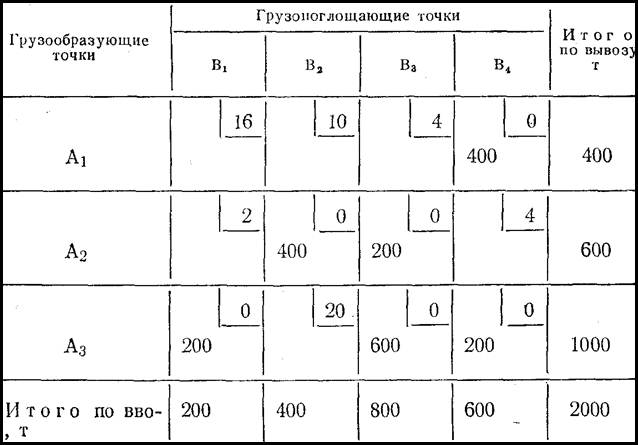
Таблица 2;

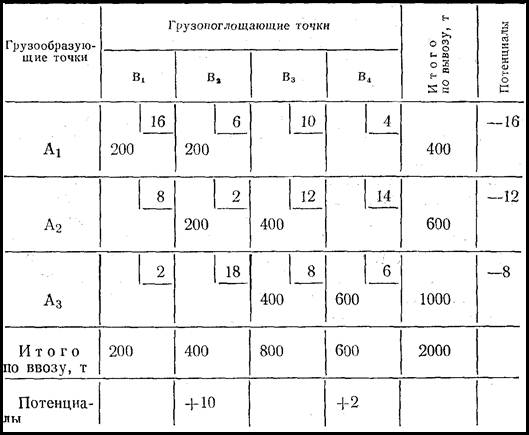
Условимся в дальнейшем называть клетки таблицы, в которых отмечено количество груза, перевозимого от грузоотправителя к данному грузополучателю, загруженными. Количество загруженных клеток всегда должно равняться величине базиса, который будет равен n + т -1 (п- число строк таблицы; т — число столбцов). В нашем примере это условие соблюдено: 3+4 — 1 = 6.

При нашем распределении груза по потребителям первой загруженной клеткой стала левая верхняя клетка А₁В₁ таблицы, остальные загруженные клетки расположились по диагонали, соединяющей левый верхний и правый нижний углы таблицы. Поэтому такой способ первоначального закрепления грузополучателей за грузоотправителями, а следовательно способ первого заполнения таблицы, получил название «диагональный метод» или «метод северо-западного угла».

Полученное таким способом закрепление потребителей груза за грузоотправителями является одним из возможных решений задачи. При этом общая грузовая работа будет равна:

200-16 + 200-6 + 200-2+400- 12 + 400-8 + 600-6 = 16400 т.км.

Однако нельзя сказать, является ли полученный вариант решения оптимальным или нет. Чтобы ответить на этот вопрос, необходимо выполнить следующие действия:

1. Во всех загруженных клетках получают нулевой потенциал.

Для этого по строчкам и столбцам табл. 2 ко всем расстояниям, проставленным в верхних правых углах клеток, прибавляются такие числа (потенциалы), которые в сумме с расстояниями загруженных клеток дают нуль (нулевой потенциал).

Например, чтобы получить в загруженной клетке А₁В₁ нулевой потенциал, нужно ко всем расстояниям строки А₁ прибавить потенциал —16 (16 – 16 = 0).

В загруженной клетке А₁В₂ нулевой потенциал получится в том случае, если к ее расстоянию 6 и ранее прибавленному по строке А₁ потенциалу —16 прибавим по столбцу В₂ потенциал +10 (6 - 16+10 = 0) и т. д.

2. Определяют потенциалы для всех свободных клеток, т. е. находят для каждой свободной клетки сумму указанного в ней расстояния с ранее полученными по загруженным клеткам потенциалами ее строки и столбца.

При решении задачи на минимум оптимальный вариант получается в том случае, когда во всех загруженных клетках стоят нулевые потенциалы, а потенциалы всех свободных клеток являются положительными. величинами.

Если задача решается на максимум, то оптимальным вариант получается тогда, когда во всех загруженных клетках стоят нулевые потенциалы, а потенциалы всем свободных клеток являются отрицательными величинами.

Наличие свободных клеток с отрицательными значениями потенциалов (при решении задачи на минимум) говорит об имеющихся резервах, использовав которые можно получить лучший вариант решения.

В первом варианте решения нашей задачи отрицательные потенциалы имеются в клетках A₁B₄; A₂B₁, А₁В₃ A₃B₁ (табл. 3). Наиболее потенциальной клеткой (клетка, имеющая наибольшее отрицательное значение потенциала) будет клетка А₁В₄, потенциал которой равен — 10.

Во втором шаге решения наиболее потенциальная клетка получает загрузку.

Это вызывает перераспределение загрузки клеток таблицы, которое осуществляется следующим образом.

1. Проверяется, чтобы количество загруженных клеток в предыдущем шаге равнялось п + т = 1.

Если количество загруженных клеток менее, чем п + т = 1, так называемый случай вырождения (см. гл. III), то недостающее число клеток получается путем загрузки соответствующего количества свободных клеток нулями. Клетка, в которой будет проставлена загрузка, равна нулю, считается загруженной.

2. Для наиболее потенциальной клетки А₁В₄ строится контур.

Контуром называется замкнутая ломаная линия, образованная прямыми отрезками, углы соединений между которыми равны 90°.

Строится контур так, чтобы все углы, кроме одного располагались в загруженных клетках, а один угол находился в свободной, наиболее потенциальной клетке.

При соблюдении этих двух правил для каждой свободной клетки можно построить только один контур.

3. Определяются положительные (+) и отрицательные (-) углы контура, считая, что первый положительный угол лежит в свободной клетке, для которой строится контур, рядом с ним находятся отрицательные углы, рядом с отрицательными — положительные и т. д.

Количество положительных углов всегда равно количеству отрицательных углов контура.

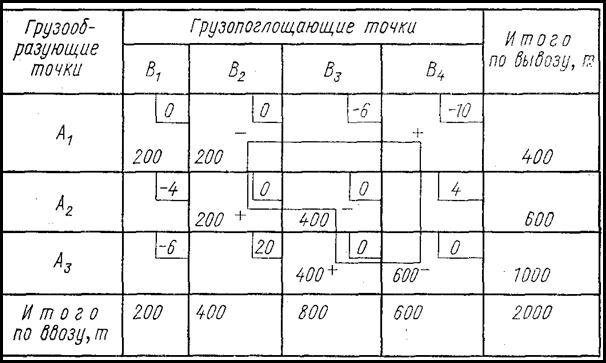Таблица 3

4. Выявляется наименее загруженная клетка, занятая отрицательным углом контура. Количество груза, указанное в этой клетке, отнимается из всех клеток, занятых отрицательными углами контура, и прибавляется во все клетки, занятые положительными углами.

В результате такого действия одна или несколько из ранее загруженных клеток становятся свободными, а наиболее потенциальная клетка становится загруженной. Ранее загруженные клетки, которые не оказались расположенными в углах контура, переносятся в таблицу (табл. 4.4) нового варианта закрепления потребителей груза за грузоотправителями без изменений.

В табл. 3 из всех клеток, занятых отрицательными углами контура, наименьшую загрузку имеет клетка А₁В₂—200 т. Эти 200 т вычитаются из всех клеток, занятых отрицательными углами контура, и прибавляются во все клетки, занятые положительными углами. В результате клетка A₁B₂ становится свободной, а наиболее потенциальная клетка А₁В₄ получает загрузку в 200 т.

Загрузка клетки A₁B₁ в которой нет угла контура, в новом варианте решения остается без изменений (см. табл. 4).

Полученный таким путем новый вариант закрепления потребителей за грузоотправителями является возможным решением задачи. При этом варианте решения общая транспортная работа будет равна

200 × 16+200 × 4 + 400 × 2 +200 × 12+600 × 8+400 × 6 = 14 400 т.км.

Это на 2000 т.км меньше, чем получено в первом варианте решения. Величину сокращения грузооборота можно определить и как произведение количества груза, которое получила наиболее потенциальная клетка, на ее потенциал [200 × (-10)]= - 2000 т.км.

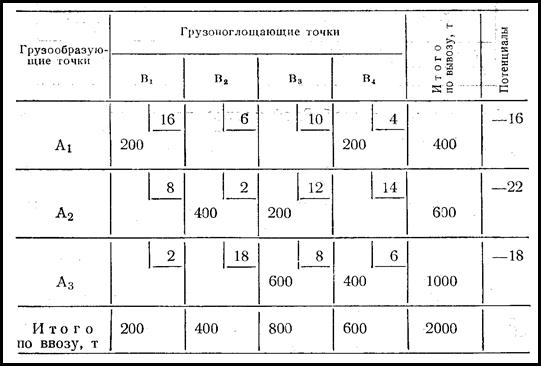Т аблица 4

+20 +10 +12

Чтобы убедиться, является ли полученный вариант оптимальным, следует повторить все действия, рассмотренные выше, т. е. нужно по новым загруженным клеткам подобрать потенциалы строк и столбцов и определить потенциалы для свободных клеток. Если вариант окажется неоптимальным, то необходимо будет построить контур для новой наиболее потенциальной клетки и найти лучший вариант решения. Задача решается до тех пор, пока не будет найден оптимальный вариант.

Количество промежуточных решений зависит от сложности задачи. В нашем примере оптимальный вариант получен в результате третьего шага решения (табл. 6). Второй же вариант, как и первый, является неоптимальным (табл. 5).

Таблица 5

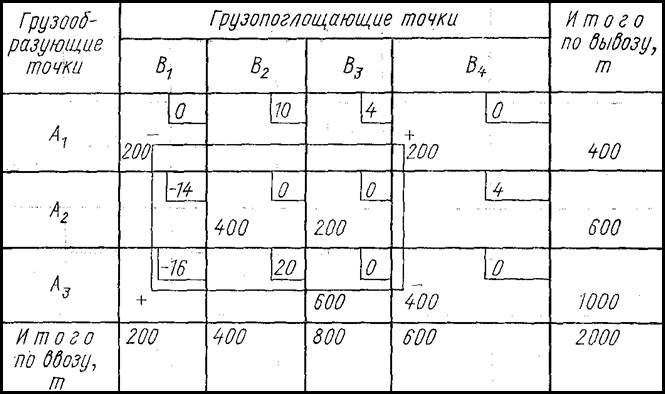
Таблица 6

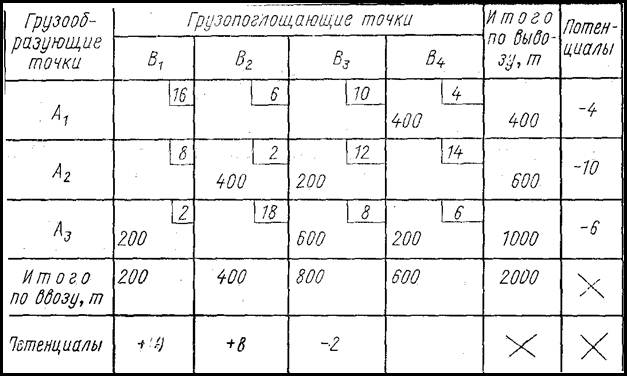
Оптимальность третьего варианта решения подтверждается тем, что во всех свободных клетках таблицы этого варианта потенциалы являются положительными величинами (табл. 7).

Таблица 7

Объем грузовой работы при оптимальном решении будет равен 11 200 ткм.

Второй способ (Метод кредо)

Третий способ (Модифицированный распределительный метод - моди)

СОКРАЩЕНИЕ КОЛИЧЕСТВА ПРОМЕЖУТОЧНЫХ РЕШЕНИЙ (ИТЕРАЦИЙ)

При решении задач распределительным методом число промежуточных решений можно значительно уменьшить, если первый вариант загрузки клеток таблицы (опорный план) произвести не по диагональному методу, а другими методами, основанными на предварительном анализе исходных данных задачи. Такие методы иногда позволяют в первом же варианте решения получить оптимальный ответ или значение, близкое к оптимальному.

Известно несколько методов сокращения промежуточных решений или, как их часто называют, методов приближенного решения.

Рассмотрим три метода: метод аппроксимации Фогеля, метод последующего анализа (метод «стрелок») и метод двойного предпочтения.

Метод аппроксимации Фогеля. Исходные данные задачи записываются в таблицу, отличающуюся от формы таблиц третьего способа тем, что она имеет дополнительно строку и столбец разностей (табл. 14).

Разницы между двумя наименьшими значениями расстояний каждой строки записываются в столбце разностей, а разницы по столбцам — в строке разностей.

Из всех разниц, полученных по строчкам и столбцам, выбирается наибольшая. Клетка с наименьшим расстоянием (при решении задачи на минимум), расположенная в столбце или строке, имеющей наибольшую разницу, загружается максимально возможным количеством груза. При этом учитывается потребность грузопоглощающей и возможности грузообразующей точек.

Если же окажется несколько одинаковых разниц, имеющих максимальные значения (строка А₂ и столбец В₁), то в соответствующих им столбцах или строчках находят и загружают седловую точку.

Таблица 14

Седловой точкой называют клетку таблицы, расстояние которой имеет наименьшее значение (при решении задачи на минимум) из всех расстояний ее строки и столбца или наибольшее значение при решении задачи на максимум.

При наличии независимых седловых точек, т. е. расположенных в различных строчках и столбцах, загружают их одновременно. Когда седловые точки отсутствуют, для строк или столбцов, имеющих максимальные одинаковые разницы, находят дополнительные разницы.

Загружается клетка с оптимальным элементом целевой матрицы, у строки или столбца которой дополнительная разница будет наибольшей.

Например, дополнительной разницей к столбцу В₁ будет разница между вторым по величине значением расстояния (8 км, клетка A₂B₁) и наименьшим расстоянием (оптимальным элементом целевой матрицы) строки А₂ (клетка А₂В₂), равная 8 - 2 = 6.

Дополнительная разница к строке А₂ будет найдена, если из второго по величине значения строки А₂ (8 км, клетка А₂В₁) отнимем наименьшее значение расстояния столбца В_І (2 км, клетка А₃В₁: 8 – 2 = 6.

Дополнительные разницы оказались равными и, следовательно, не дают возможности определения преимущества загрузки какой-либо из точек. Можно было бы произвольно загрузить любую из точек, оптимальных для строки А₂ или столбца В₁ но это не всегда поможет уменьшить число шагов решения, которое в дальнейшем будет производиться распределительным методом. В таком случае следует определить аналогичным путем вторую дополнительную разницу к выбранным столбцам или строчкам.

В данном примере второй дополнительной разницей к столбцу В₁ будет разница между третьим по величине значением расстояния, стоящим в клетках столбца (клетка А₁В₁, 16 км), и наименьшим значением расстояния в строке А₁ (клетка А₁В₄, 4 км), которая равна 16 - 4 = 12.

Вторая дополнительная разница к строке А₂ будет найдена, если из расстояния клетки А₂В₃ (12 км) вычесть расстояние клетки А₃В₃ (8 км): 12 - 8 = 4.

Загружается в первую очередь та из оптимальных точек, у столбца или строки которой какая-либо из дополнительных разниц имеет наибольшее значение.

В нашем примере нет необходимости находить дополнительные разницы, поскольку имеются две независимых седловых точки (А₃В₁ и А₂В₂), которые можно загрузить одновременно с учетом имеющихся ограничений по спросу и предложению (табл. 15). Оставшиеся клетки столбцов В₁ и В₂ отмечаются знаком «X». Разницы столбцов В₁ и В₂ перечеркиваются, и ставится знак «К», означающий, что в данных столбцах распределение груза окончено. Затем определяются новые разницы для всех строк и столбцов. При этом загруженные клетки и свободные клетки, отмеченные знаком «X», не берутся во внимание. Если вновь полученные разницы отличаются от полученных ранее, то последние зачеркиваются, а рядом с ними записываются новые значения. Далее действия повторяются, пока весь груз не будет распределен. Последние одна или две клетки загружаются без определения разностей.

Полученный по методу аппроксимации Фогеля вариант решения проверяется на оптимальность с соблюдением правила модифицированного распределительного метода. Если он оказывается неоптимальным, то дальнейшее решение производится по алгоритму модифицированного распределительного метода.

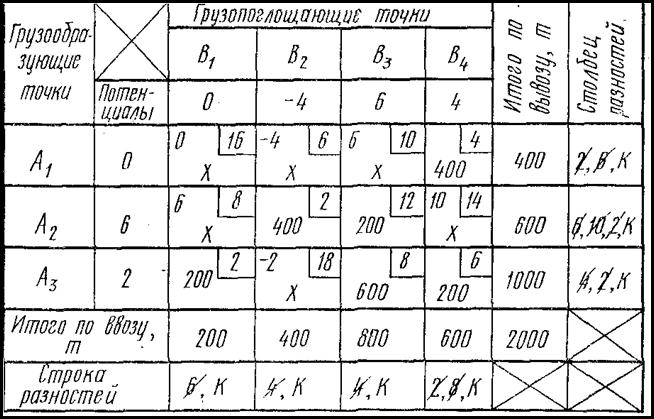Таблица 15

В данном случае распределение груза, произведенное по методу аппроксимации Фогеля, является оптимальным решением (см. табл. 15).

Метод последующего анализа (метод «стрелок»). Рассмотрим этот метод на задаче, исходные данные которой записаны в табл. 16.

Закрепление потребителей за грузоотправителями, начиная с первого потребителя (столбец В₁), производится с учетом наименее возможного расстояния перевозки. При этом учитываются не только потребности потребителей, но и наличие груза у грузоотправителей. Полученное таким путем первое решение анализируется с целью выявления возможностей его улучшения.

В строке А₁ можно передвинуть из клетки А₁В₄, имеющей расстояние 8 км, 150 т груза в клетку А₁В₁ срасстоянием 7 км и 100 т груза в клетку А₁В₂ с расстоянием 5 км.

В результате этого расстояние перевозки груза из точки А₁ сократится в первом случае на 1 км, а во втором —-на 3 км.

Вместо передвинутых 250 т груза из клетки А₁В₄ следует переместить в клетку А₂В₄ и А₃В₄ соответствующее количество груза из клеток А₁ и А₃В₂. Эта передвижка также позволяет сократить расстояние перевозки груза потребителем из точек А₂ и А3. Анализируя оставшиеся загруженные клетки, можно убедиться в целесообразности перемещения 100 т груза из клетки А₁В₃ в клетку А1В₂ вместо них столбец В₃ получит загрузку из клетки А₂В₂, загрузится клетка А₂В₃.

Таблица 16 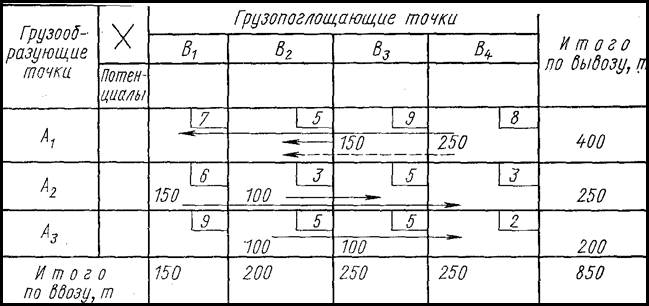І

Хотя перемещение загрузки из клетки А₂В₂ в клетку А₂В₃ повлечет за собой увеличение расстояния перевозки на 2 км, сокращение расстояния на 4 км в результате передвижки груза из А₁В₃ в А₁В₂ даст общее уменьшение расстояния на 2 км.

Закончив улучшение плана поставок за счет перемещения их в клетки с меньшим расстоянием по строкам матрицы (см. табл. 16), переходят к рассмотрению возможности улучшения решения путем передвижения загрузок клеток по столбцам (табл. 4.17).

В данном случае по столбцу В₄ следует переместить из клетки А₂В₄ 100 т в клетку А₃В₄, одновременно передвинув такое же количество груза по столбцу В₃ из А₃В₃ в А₂В₃.

Следует иметь в виду, что передвижение будет рационально, если сумма расстояний, указанных в углах клеток, из которых перемещается загрузка, будет больше, чем сумма расстояний клеток, в которые передвигается загрузка.

Последующий анализ строк и столбцов таблицы показывает, что загрузка находится в клетках с наименьшим расстоянием и передвигать ее нецелесообразно. Проверяя полученный вариант закрепления потребителей за грузообразующими точками с помощью модифицированного распределительного метода, убеждаемся в оптимальности решения (табл. 18).

Если оптимальный вариант не найден, то дальнейшее решение производится обычным путем с помощью распределительного метода.

Таблица 4.17

При решении задач настоящим методом можно встретиться со случаем, когда число загруженных клеток в последнем распределении окажется большим, чем п +т - 1, и при проверке оптимальности решения неизбежно для какой-либо строки или столбца таблицы будут найдены два потенциала, которые не позволят осуществить правильное решение. Чтобы устранить такую ситуацию в распределении поставок, нужно произвести следующие действия:

1. Построить для загруженной клетки, по которой одновременно определяются два потенциала, контур так, чтобы все его углы лежали в загруженных клетках.

2. Углы контура обозначить попеременно знаками «+» и «-».

Углу, лежащему в загруженной клетке, для которой построен контур, первому придается знак «+».

3. Выявить наименьшую загрузку в клетках, запятых углами контура со знаком «+». Вычесть ее из всех этих клеток и прибавить во все клетки, занятые углами со знаком «-».

В результате таких действий количество загруженных клеток сократится. При этом ранее найденное распределение не ухудшится. Оно или будет улучшено или останется неизменным.

Метод «стрелок» более рационально применять при решении задач, требующих построения небольших матриц. Когда же требуется построение таблиц со значительным числом клеток, наименее трудоемким оказывается метод аппроксимации Фогеля.

Таблица 18

Метод двойного предпочтения. В основе этого метода лежит анализ элементов целевой матрицы — по строчкам и столбцам таблицы, в процессе которого выявляются клетки с оптимальным (как по строке, так и по столбцу) элементом. Эти клетки отмечаются каким-либо знаком (*) и загружаются с учетом ограничений по спросу и предложению, после чего свободные клетки строчек и столбцов, исчерпавших свои возможности, зачеркиваются (табл. 19).

Таблица 19

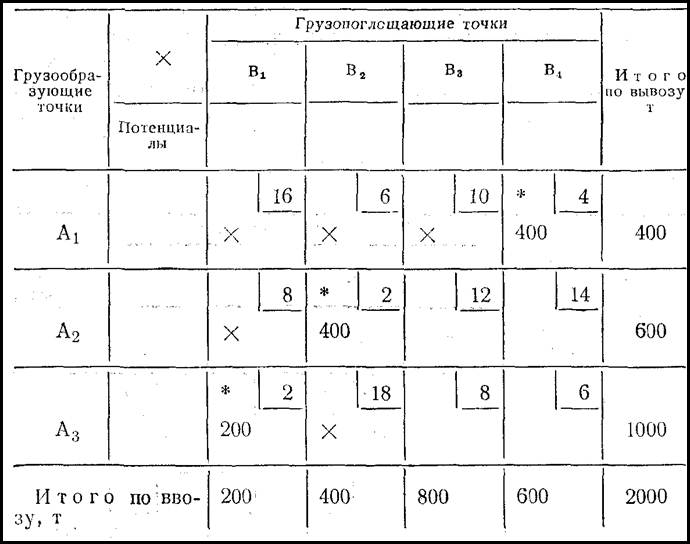
Таблица 20

Затем те же самые действия повторяют со строчками и столбцами, ограничения которых еще позволяют производить распределения, не принимая во внимание ранее загруженные и вычеркнутые свободные клетки (табл. 20). Построение опорного плана (первого возможного базисного варианта решения) будет закончено, когда будут исчерпаны все ограничения по предложению и удовлетворен весь спрос (табл. 21).

Таблица 4.21

Дальнейшее решение производится по алгоритму распределительного метода.

Опорный план, построенный по методу двойного предпочтения, в данном.примере является оптимальным решением, в чем нетрудно убедиться, проверив его методом моди.