Общие понятия о симплексном методе

СИМПЛЕКСНЫЙ МЕТОД

ГРАФАНАЛИТИЧЕСКИЙ МЕТОД

Графоаналитический метод является одним из простейших методов линейного программирования. Он наглядно раскрывает сущность линейного программирования, геометрическую интерпретацию его методов. Однако этот метод имеет существенный недостаток: с его помощью можно решить только те планово-экономические задачи, математическая модель которых представляет собой систему с двумя неизвестными величинами. По этой причине в организации и планировании перевозок автомобильным транспортом этот метод может быть применен для решения очень узкого круга задач.

Одним из самых распространенных методов решения задач линейного программирования является симплексный метод.

Свое название метод получил от слова «симплекс», обозначающего простейший выпуклый многогранник, число вершин которого всегда на единицу больше, чем размерность пространства. На плоскости (двухмерное пространство) симплексом является треугольник, в трехмерном пространстве — четырехгранник и т. д.

Симплексный метод применяется в планировании ассортимента выпускаемой продукции, оптимальной загрузки оборудования, в решении технологических и транспортных задач, имеющих линейные математические модели.

Идея симплексного метода состоит в следующем. Пусть задача линейного программирования заключается в том, чтобы найти неотрицательные значения переменных х₁, х₂, х_з, х ₄, которые обращают в минимум линейную форму

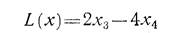
при условиях

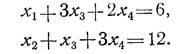
Систему ограничений можно разрешить относительно переменных х₁ и х₂, которые и будут составлять базис:

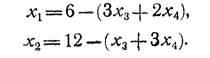
исходя из условия неотрицательности, имеем наименьшие значения свободных переменных: х_з = 0; х ₄ = 0. При этом значения базисных переменных: х ₁ = 6; х ₂ = 12. Все значения переменных положительны, а потому совокупность х ₁ = 6; х ₂=12; х ₃ = 0; х ₄ = 0 является допустимым решением системы. Значение целевой функции при этом базисе равно нулю.

Посмотрим, нельзя ли уменьшить значение линейной формы L(x). Переменная х ₃ входит в нее с положительным знаком, поэтому увеличивать х ₃ нет смысла, так как это привело бы к увеличению L(x). Оставим х ₃ равным нулю. Увеличение свободной переменной х ₄ ведет к уменьшению L(x), поскольку х ₄ входит в линейную форму с отрицательным знаком.

Переменные связаны с системой линейных уравнений и подчинены условию неотрицательности. В связи с этим увеличивать х ₄ неограниченно нельзя, так как, например, при х ₄ = 4 (х ₃ = 0) из первого уравнения базисной системы х ₁ = —2 < 0, т. е. при этом нарушается условие неотрицательности переменных и решение становится недопустимым.

Очевидно, чтобы найти максимально возможное значение х ₄, обеспечи-вающее допустимое решение задачи, нужно составить отношение свободных членов к положительным коэффициентам при х ₄ и из них выбрать наименьшее. Из первого уравнения исходной системы это отношение равно 6: 2 = 3; из второго - 12: 3 = 4. Следовательно, максимальное значение х ₄, при котором решение системы остается допустимым, равно 3. Тогда х₁ = 6 - (3 х ₃ + 2 х ₄) = 6 - 6 = 0; х ₂ = 12 - (х ₃ + 3 х ₄) = 12 - 9 = 3. Поскольку только базис дает решение системы, то х ₄ следует принять за базисную переменную, заменив им х _1. Итак, новый базис х ₂ и х ₄, а свободные переменные х ₁ х ₃. Новое допустимое решение: х ₁ = 0; х ₂ = 3; х ₃ = 0, х ₄ = 3. Значение целевой функции при новом базисе уменьшилось:

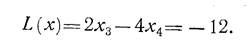
Переход к новому базису осуществляется на основе исключения новой базисной переменной из всех уравнений, кроме одного, в которое эта переменная должна входить с коэффициентом, равным единице. Элементарными Преобразованиями системы исключим х₄ из второго уравнения:

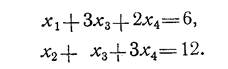
В исходной системе умножим второе уравнение на 2 и вычтем из него утроенное первое уравнение, получим новую, эквивалентную предыдущей систему

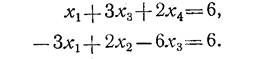
Разделив каждое уравнение на коэффициент при х₄, получим:

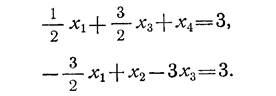
Отсюда найдем новое базисное решение:

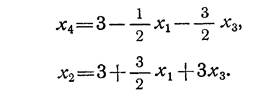
При этом

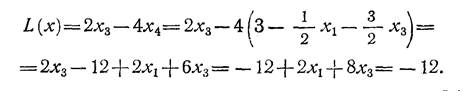Вспомогательные переменные х₁ и x₃ входят в L(x) с положительными коэф-фициентами. Поэтому наименьшие возможные значения для них: х₁ = 0; х_ъ = 0. В базисе х₂ и х ₄ линейная форма достигает своего минимума:

L(x _{) min} = — 12.

Следовательно, чтобы получить неотрицательные базисные решения системы линейных уравнений, надо процесс исключения неизвестных вести так, чтобы свободные члены всех уравнений на всех этапах процесса оставались неотрицательными. При этом руководствуются следующим правилом: в качестве новой базисной переменной принимается любая свободная переменная, при которой есть хотя бы один положительный коэффициент; выводится из базиса переменная, которая соответствует наименьшему отношению свободных членов уравнений к соответствующим положительным коэффициентам при вводимой в базис переменной. Такие преобразования называются симплексными преобразованиями.

Это очень важно, так как для нахождения частного неотрицательного решения, отвечающего наибольшему возможному значению какой-то одной свободной переменной при нулевых значениях других свободных переменных, вместо определения области изменения указанной переменной и подставления ее наибольшего возможного значения в общее решение достаточно принять указанную переменную за базисную и подвергнуть систему симплексному преобразованию, перейдя к новому базису, что значительно упрощает расчеты.

Вычисления удобно производить с помощью симплексных таблиц. Переход от одной таблицы к другой соответствует одной итерации, т. е. переходу от одного базиса к другому, при этом значение целевой функции уменьшается. За конечное число итераций переходят к базису, для которого получают минимальное (максимальное) значение целевой функции; соответствующее ей базисное допустимое решение и является оптимальным (если задача имеет решение).