2014-02-02
483
Покажем, что точка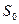 
, определяющая минимаксную стратегию второго игрока, является граничной точкой области 
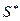, причем такой, в которой область T касается области .
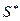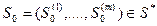, причем 
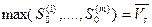. С другой стороны 
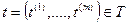, если 
, 
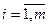это множество m-мерных векторов, каждая из координат которых не превышает верхней цены игры.
Рассмотрим точку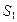 
, которая связана с точкой 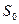следующим образом:
, 
, 
, .
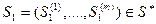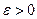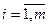Очевидно, что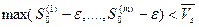 
, поэтому 
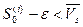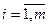, . Значит, 
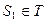. Но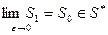 
.
Из этого следует два вывода:
1) точка 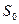— граничная точка области ;
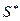2) 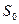— точка, в которой область T касается области .
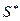Эти свойства позволяют легко находить геометрически минимаксную стратегию 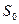для случая, когда первый игрок имеет две чистые стратегии, т.е. когда эквивалентная S-игра изображается множеством точек плоскости. Для построения области T, касательной к области 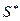, удобно провести вспомогательную прямую из начала координат под углом 
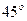к оси абсцисс, на которой лежит вершина прямоугольного клина, образующего область T.
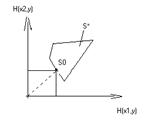
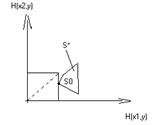
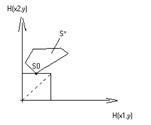
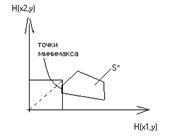
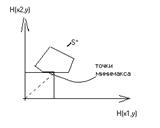
На рисунке приведены различные случаи взаимного расположения областей 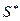и T и отмечены точки, определяющие минимаксную стратегию второго игрока 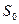, и множества минимаксных стратегий второго игрока.
