Игры с частными случаями платежных матриц

При анализе игры используются следующие свойства платежных матриц:

1) Произведение матрицы на число.

, , , .

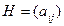
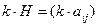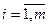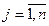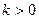Стратегии игроков не меняются, увеличивается только цена игры

.

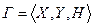
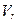
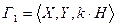
При получается проигрыш.

2) Прибавляем к элементам матрицы положительное число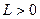

,

,

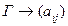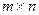
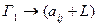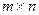
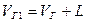, оптимальные стратегии не меняются.

Латинский квадрат.

Латинским квадратом называют матрицу 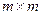, если каждая из ее строк (столбцов) состоит из чисел от 1 до m.

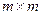
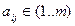
Пример:

.

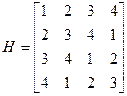Для таких матриц справедливо следующее соотношение, определяющее цену игры: 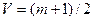. В данном примере цена игры равна 2,5.

Диагональная игра.

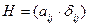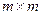, , где 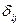— символ Кронекера.

При такой матрице диагональные элементы можно преобразовать в . В оптимальные стратегиях игроков входят все чистые стратегии .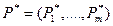

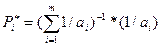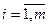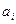, , — диагональные элементы.

Аналогично для второго игрока:

.

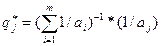Пример:

2 кг ершей, 3 кг щуки. С какой вероятностью надо выбирать поход за ершами?

.

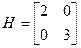
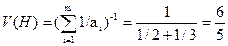
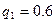
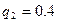Делаем вывод, что за ершами надо ходить чаще.

Если все 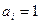, то , .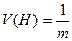

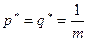Игра, у которой диагональные элементы равны -1, а остальные равны 1.

Пусть матрица выигрышей имеет произвольный порядок m:

, , .

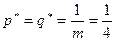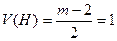Для диагональных игр все стратегии являются рабочими (полезными), в других играх число полезных стратегий .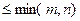

Теорема о поведении игроков. Если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш игроков неизменен и равен цене игры, если второй игрок не выходит за пределы своих полезных (рабочих) стратегий. Размер выигрыша не зависит от того, какую из чистых или смешанных стратегий он использует.