Решение матричных игр
Существует несколько основных методов решения матричных игр:
1. Аналитический
2. Графический
3. Итеративный (метод Брауна-Джонсона)
4. Метод линейного программирования
Рассмотрим подробнее последний из перечисленных.
Пусть имеется некоторая матричная игра Г=<X,Y,H> (где X и Y — множества стратегий 1го и 2го игроков соответственно, а Н — платежная матрица),  H=(aij)
H=(aij) 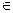 Rm*n
Rm*n
Требуется найти оптимальную смешанную стратегию, т.е.
p*=(p1*,p2*,…,pm*) и q*=(q1*,q2*,…,qn*), при которых
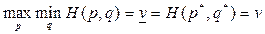
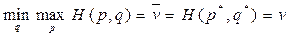 ,
,
где v — цена игры.
Для решения этой задачи можно применять линейное программирование.
Будем считать, что все aij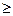 0, игра Г’ эквивалентна игре Г, H’=H+L, L — число, при котором неравенство будет выполняться (при переходе от игры Г к игре Г’).
0, игра Г’ эквивалентна игре Г, H’=H+L, L — число, при котором неравенство будет выполняться (при переходе от игры Г к игре Г’).
Далее предположим, что 2й игрок принимает стратегию yk, 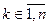 , тогда выигрыш игрока 1 будет определяться условием
, тогда выигрыш игрока 1 будет определяться условием
p1a1k + p2a2k + … + pmamk 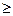 v,
v, 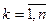 (*)
(*)
(равенство v достигается, если k-я стратегия является рабочей)
pi 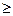 0,
0, 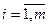 ;
; pi aik > 0
pi aik > 0 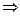 v>0 (т.к. левая часть неравенства (*) больше нуля).
v>0 (т.к. левая часть неравенства (*) больше нуля).
Разделим неравенство (*) на v:
t1a1k + t2a2k +…+ tmamk 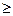 1, где ti=
1, где ti=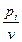 , ti
, ti 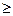 0,
0, 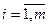
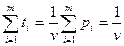
Цель стратегии 1-го игрока — максимизировать выигрыш:
v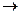 max
max 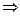

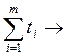 min
min
Исходя из рассмотренных условий, задачу линейного программирования можно сформулировать так:
1) ti 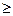 0,
0, 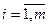
2) 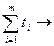 min
min
3) 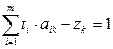 , причем zk=0 для рабочих стратегий, zk>0 для нерабочих стратегий.
, причем zk=0 для рабочих стратегий, zk>0 для нерабочих стратегий.
Решение этой задачи позволяет:
1. Вычислить ti*.
2. Определить те k, при которых zk=0 (т.е. найти рабочие стратегии 2го игрока)
3. 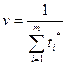
4. pi*=ti* v
Для определения стратегии 2го игрока можно поступить двояко:
1) сформулировать двойственную задачу
2) использовать информацию о полезных стратегиях 2-го игрока (полезные стратегии – при zk=0)
Пусть найдена полезная стратегия игрока yj, 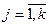 ,
, 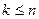 . Для определения оптимальной стратегии qj*,
. Для определения оптимальной стратегии qj*, 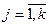 для рабочих стратегий 1-го игрока можно записать условие
для рабочих стратегий 1-го игрока можно записать условие
q1ai1 + q2ai2 + … + qkaik 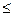 v,
v, 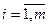
(причем если i-я стратегия 1-го игрока рабочая, то =v,а если нет, то >v)
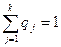 q1ai1 + q2ai2 + … + qkaik
q1ai1 + q2ai2 + … + qkaik 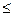 v,
v, 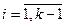
- система уравнений для определения оптимального q.
 2014-02-02
2014-02-02 855
855








