Пример: Графическое решение игр 2*n и m*2

Пусть имеется некоторая игра с матрицей A=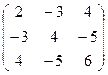

A+5 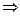A₁=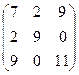

Предположим, что все стратегии рабочие. Составляем систему уравнений:

7t₁ + 2t₂ + 9t₃ - z₁ = 1

2t₁ + 9t₂ - z₂ = 1

9t₁+11t₃ - z₃ = 1

Решение этих уравнений при условии t₁ + t₂ + t₃ 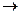min:

t₁ = 0,05

t₂ = 0,1

t₃ = 0,05

v(A₁) =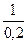= 5 p₁=0,05*5=0,25

p₂=0,1*5=0,5

p₃=0,05*5=0,25

v(A)=v(A₁) - 5=0 игра справедливая. Найдём стратегию второго игрока:

q₁^* + q₂^* + q₃^* = 1

2q₁ + 9q₂ = 5 q₁=q₃=0,25

9q₁ + 11q₃ =5 q₂=0,5

Графическое решение игр 2*n и m*2

Рассмотрим игру (2*n) с матрицей

A=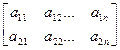

Выигрыш 1-го игрока H(p,y_k)=p₁a_1k + p₂a_2k = p₁a_1k + (1-p₁)a_2k,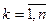

На плоскости такая зависимость изображается отрезком прямой, причем при p=0 H(p,y_k)=a_2k, p=1 H(p,y_k)=a_1k

Таким образом, получаем семейство из n прямых:

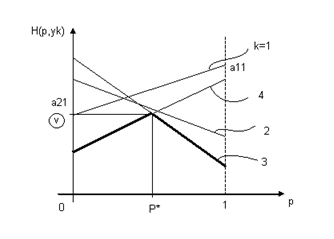
Исходя из условия гарантированного выигрыша, его величина при разных значениях р будет определяться нижней границей множества этих прямых. Очевидно, что оптимальная стратегия соответствует той точке полученного множества, в которой значение функции максимально, а само это максимальное значение есть значение игры.

Рабочими стратегиями 2-ого игрока являются в данном случае 3я и 4я, а значит, оптимальная стратегия 1-ого игрока определяется из системы уравнений:

q₃ + q₄ = 1

a₂₃q₃ + a₂₄q₄ = v

Рассмотрим теперь игру (m*2) с матрицей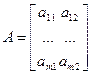

Эту игру удобно рассматривать для второго игрока. Как и в предыдущем случае, строится семейство из m отрезков прямых, отображающих зависимость величины функции выигрыша 2го игрока от выбираемой им стратегии:

Н(x_i,q)= a_i1q + a_i2(1-q), ,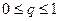

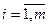
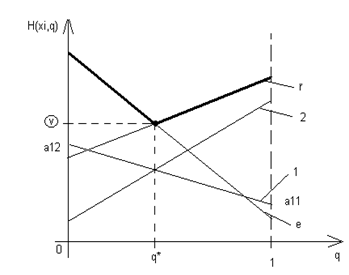
Исходя из разумности поведения 1-ого игрока, проигрыш 2-ого определяется верхней огибающей семейства этих прямых. Значения q* и v находятся как абсцисса и ордината нижней вершины огибающей, а затем оптимальная стратегия 2-ого игрока определяется исходя из его рабочих стратегий (в данном случае рабочими стратегиями 2-ого игрока являются x_r и x_e), аналогично предыдущему случаю.

Во всех этих случаях число рабочих стратегий обоих игроков одинаково.