Принципы оптимальности в бескоалиционных играх

Ранее рассматривались антагонистические игры, у которых принцип минимакса и принцип равновесия совпадают. Это совпадение определяет единое понятие оптимальности и решения игры. В теории неантагонистических игр нет единого подхода к выработке принципа оптимальности. В литературе имеется множество таких принципов, каждый из которых требует своих особых предположений о поведении игроков и о структуре игры. Предположим, что в игре Г каждый из игроков стремится к ситуации Х=(х⁽¹⁾,…,х^(N)), при которой максимизируется его выигрыш: H_i(x)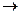max. Но для других игроков эта ситуация может приводить к противоречивому результату: H_j(x)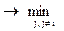. Для оценки качества ситуаций x⁽¹⁾…x^(N) часто используется принцип равновесия по Нэшу и его различные обобщения.

Пусть х=(x⁽¹⁾… x⁽ⁱ⁾,x⁽ⁱ⁺¹⁾…x^(N)) — произвольная ситуация в игре Г, а x⁽ⁱ⁾ — некоторая стратегия игрока i. Обозначим через (x//x₁⁽ⁱ⁾) ситуацию, которая отлична от х только тем, что стратегия x⁽ⁱ⁾ заменена на x₁⁽ⁱ⁾. Тогда выражение

H_i(x//x₁⁽ⁱ⁾)=Н(x⁽¹⁾… x₁⁽ⁱ⁾,x⁽ⁱ⁺¹⁾…x^(N)) определяет выигрыш i-ого игрока при такой замене.

Ситуация x*=(x₁*…x_N*) называется ситуацией равновесия по Нэшу, если для всех x_i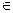X_i и 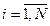верно неравенство:

H_i(x*) 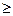H_i(x*//x⁽ⁱ⁾)

Т.е. всякое отклонение от ситуации равновесия ведет к снижению выигрыша.

Если ситуация x* достигнута путем предварительной договоренности, то никому из участников договора не выгодно изменять его условия.

Стратегия x_k⁽ⁱ⁾ (k-ая стратегия i-ого игрока), входящая хотя бы в одну из ситуаций равновесия по Нэшу, называется равновесной.

Рассмотрим игру Г=<x₁,x₂,H₁,H₂>. Для бескоалиционной игры двух лиц ситуация x₁*,x₂* называется ситуацией равновесия, если

H₁(x₁,x₂*)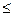H₁(x₁*,x₂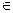*), x₁X₁

H₂(x₁*,x₂)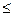H₁(x₁*,x₂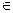*), x₂X₂

Для матричной игры, где H₁=(a_ij) m*n, H₂=(b_ij) m*n условия равновесия по Нэшу имею вид:

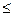a_ij* a_i*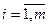j*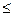

b_ij* b_i*j*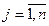

Особенности ситуации в матричной игре рассмотрим на примере игры «семейный спор».

2 игрока — муж и жена — решают, как провести вечер. Ситуация описывается следующей матрицей:

м ж

а₁₁=4 b₁₁=1 (— “пойти на боксерский матч”)

а₂₂=1 b₂₂=4 (— “пойти на показ мод”)

0 0 (— если не договорятся и никуда не пойдут)

A/B=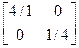

В данном случае ситуации x_1,y₁ и x_2,y₂, где наблюдается наибольший выигрыш, не являются ситуациями равновесия по Нэшу, т.к. один из игроков в этих ситуациях имеет возможность увеличить свой выигрыш путем изменения своей стратегии на противоположную.

Другим принципом оптимальности в бескоалиционных играх является принцип оптимальности по Парето.