Функция φ(x) называется выпуклой, если для любых двух точек x1 и x2 из множества X выполняется неравенство:
φ(λx1 + (1-λ)x2 )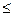 λφ(x1) + (1- λ)φ(x2),
λφ(x1) + (1- λ)φ(x2), 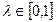
Если неравенство строгое, то и функция строго выпуклая (если неравенство выполняется строго, то вторая производная φ˝(x)>0).
Опр. Игра Г=<X,Y,a> называется игрой на единичном квадрате, если X=[0,1] и Y=[0,1], а целевая функция a(x,y) определена на каждой точки этого квадрата.
Опр. Игра Г на единичном квадрате называется непрерывной, если функция платежей a(x,y) непрерывна в каждой точке единичного квадрата по обеим переменным.
Опр. Непрерывная антагонистическая игра на единичном квадрате называется выпуклой, если функция a(x,y) строго выпукла по Y для всех x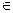 X. Иными словами, для функции платежей в строго выпуклой игре имеет место неравенство:
X. Иными словами, для функции платежей в строго выпуклой игре имеет место неравенство:
a(x, λy1 + (1-λ)y2) < λ a(x,y1) + (1- λ) a(x,y2), 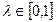 .
.
Исходя из свойств строгой выпуклости, 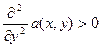
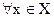 .
.
Теорема. В строго выпуклой игре на единичном квадрате 2-ой игрок имеет единственную оптимальную стратегию, которая является чистой. Цена игры в этом случае v(a), где а — функция платежей.
v(a) = 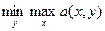 =
= 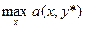 , где y* — оптимальная чистая стратегия 2-го игрока.
, где y* — оптимальная чистая стратегия 2-го игрока.
Х* — подмножество стратегий 1-го игрока, состоящее из тех х*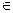 Х, для которых выполняется условие a(x*,y*) = v(a).
Х, для которых выполняется условие a(x*,y*) = v(a).
х* — тоже чистые стратегии, они называются существенными стратегиями, а остальные – несущественными.
Нахождение существенных стратегий 1-ого игрока основано на выполнении следующих свойств.
1. Если y*=1, то у 1-го игрока существует стратегия х1, для которой
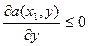 .
.
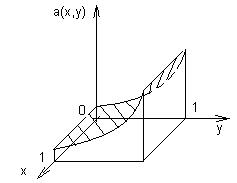
Геометрическое истолкование:
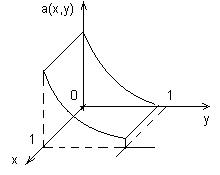
При уменьшении y a(x,y) возрастает.
2. Если y*=0, то среди стратегий 1-го игрока существует такая стратегия х2, что 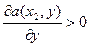 , y=y*.
, y=y*.
3. Если имеется значение стратегии 0<y*<1, то у 1-го игрока найдутся 2 существенные стратегии х1 и х2,для которых имеет место условие
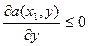 , y=y*
, y=y* 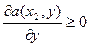 , y=y*
, y=y*
Наиболее оптимальной стратегией 1-ого игрока является вероятностная смесь стратегий х1 и х2, причем х1 — с вероятностью р, х2 — с вероятностью (1-р). При этом выполняется условие
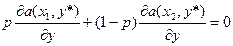 — уравнение, позволяющее определить р.
— уравнение, позволяющее определить р.
Доказывается, что решение этого уравнения единственно и принадлежит интервалу 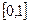 .
.
Пример. Пусть имеется игра Г=<X,Y,a>, x,y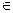 [0,1], функция выигрыша a(x,y) = (x-y)2.
[0,1], функция выигрыша a(x,y) = (x-y)2.
1). Рисуем график функции платежей (выигрыша):
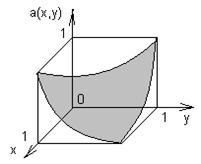
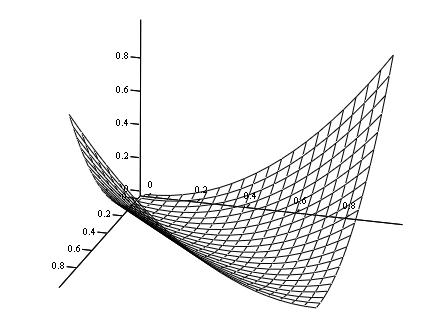
2). Проверим функцию платежей на выпуклость.
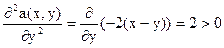
Функция платежей строго выпукла по у. Имеем дело со строго выпуклой игрой на единичном квадрате.
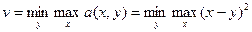
Найдем v=v(a). Для этого рассмотрим функцию:
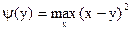 .
.
Построим таблицу:
| y | 0.25 | 0.5 | 0.75 | ||
| Ψ(y) | 0.5625 | 0.25 | 0.05625 |
y*=0.5
v(a)=0.25
Отсюда видим, что в нашем случае 0<y*<1, а следовательно, у 1-го игрока есть две существенные стратегии: х1 и х2. Для их нахождения рассмотрим зависимость
v(a)=a(x,y*)=(x-y*)2=(x-0.5)2=0.25
x1=0, x2=1 — две существенных чистых стратегии 1-го игрока.
Проверим, что эти решения действительно являются существенными стратегиями (проверка на противоположность производных).
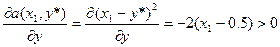
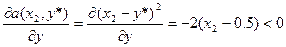
следовательно, оптимальная стратегия 1-го игрока есть вероятностная смесь по стратегиям х=х1 и х=х2. Найдем эти вероятности.
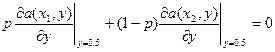
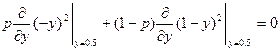
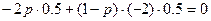
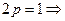 p=0.5
p=0.5
Покажем, что найденное решение является точкой равновесия. Рассмотрим проигрыши 2-ого игрока при оптимальной стратегии 1-ого:
a(x*,y) = p*(x1 - y)2 + (1-p*)(x2 - y)2 = 1/2(-y)2 + 1/2(1-y)2 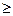
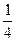 ,
,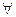 y, следовательно минимум 1/4.
y, следовательно минимум 1/4.
a(x,y*) — выигрыш 1-ого игрока при условии, что 2-ой примет свою оптимальную чистую стратегию.
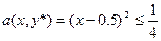
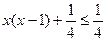
 2014-02-02
2014-02-02 1130
1130








