Рис. 2.1. К понятию о силе Рис. 2.2. Направления силы
тяжести Земли тяжести Земли
- 6 -
Вектор силы F направлен приблизительно к центру Земли. Наи-большее значение сила F имеет на полюсах и наименьшее – на экваторе. Сила P имеет максимальное значение на экваторе, где она составляет приблизительно 1:288 от величины F. На полюсах сила P равна нулю. Следовательно, сила G на земной поверхности непрерывно увеличивается от экватора к полюсам и на полюсах имеет максимальное значение. В свою очередь сила земного притяжения F есть равнодействующая притяжений всех масс, заключенных в теле Земли. Значит, величина и направление силы обусловлены распределением этих масс. Отсюда следует, что и направление отвесной линии тоже зависит от распределения масс в теле Земли.
Из курса физики известно, что в гравитационном поле Земли работа силы тяжести не зависит от формы пути MN (рис. 2.3), а зависит только от положения начальной и конечной точек этого пути. Поле, обладающее таким свойством, называется потенциальным. Во всяком потенциальном поле можно провести так называемые уровенные поверхности, т.е. такие поверхности, при движении материальной точки по которым сила поля работы не совершает. Нетрудно доказать, что в гравитационном поле Земли расстояние между уровенными поверхностями убывает к полюсам.
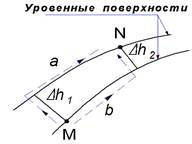
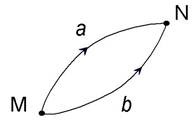
Рис. 2.3. К понятию о Рис. 2.4. Непараллельность
работе силы тяжести уровенных поверхностей
- 7 -
Возьмём две точки M и N в плоскости земного меридиана, лежа-щие на разных, но близких одна к другой, уровенных поверхностях (рис. 2.4). Согласно сказанному выше о работе силы тяжести, можем написать выражения для работы по пути MaN и по пути MbN и приравнять их: 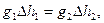
где ∆ h 1 и ∆h 2 - расстояния между уровенными поверхностями,
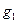 и
и 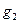 - величины ускорений силы тяжести в точках M и N.
- величины ускорений силы тяжести в точках M и N.
 Сила тяжести G возрастает к полюсам, следовательно,
Сила тяжести G возрастает к полюсам, следовательно, >
> . Поэтому из равенства легко увидеть, что
. Поэтому из равенства легко увидеть, что  <
<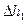 . Вывод: уровенные поверхности гравитационного поля Земли между собой непараллельны и расстояние между ними уменьшается к полюсам.
. Вывод: уровенные поверхности гравитационного поля Земли между собой непараллельны и расстояние между ними уменьшается к полюсам.
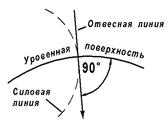
Рис. 2.5. Уровенные поверхности Рис. 2.6. Направление
и силовые линии гравитационного отвесной линии
поля Земли
Линии, нормальные к уровенным поверхностям, называются силовыми линиями (см. рис. 2.5). Касательная к силовой линии в данной точке есть отвесная линия в этой точке. Следовательно, отвесная линия является нормалью к уровенной поверхности (рис. 2.6). Поверхность воды в спокойном состоянии является одной из уровенных поверхностей. Можно провести бесчисленное множество уровенных поверхностей; каждая из них вблизи земной поверхности будет поверхностью неразрывной, замкнутой, без складок и рёбер. Вид уровенной поверхности зависит от распределения масс в теле Земли.
- 8 -
При равномерном распределении масс (см. рис. 2.7) эта поверхность будет занимать положение, показанное пунктиром. При наличии массы M с преувеличенной плотностью уровенная поверхность будет иметь некоторый выгиб кверху.
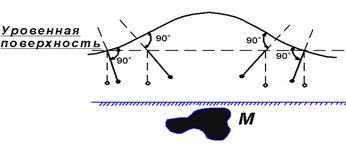
Рис. 2.7. Вид уровенной поверхности
2.2. Основная уровенная поверхность. Геоид. Эллипсоид.
Как отмечалось выше, геодезические измерения связаны с направлением отвесной линии в тех точках, в которых они выполнялись. Значит, в каждой такой точке результаты измерений могут быть отнесены именно к той уровенной поверхности, которая проходит через данную точку. Но в таком случае результаты измерений на пунктах какой-либо геодезической сети окажутся отнесенными к различным уровенным поверхностям и замкнутых фигур в сети не образуется. В связи с этим возникает необходимость приведения результатов всех геодезических измерений прежде всего к некоторой данной или принятой в качестве общей исходной уровенной поверхности. В качестве основной уровенной поверхности Земли принята поверхность вод морей и океанов в их невозмущенном (спокойном) состоянии, мысленно продолженная под материками таким образом, что в любой ее точке она нормальна (перпендикулярна) отвесной линии в этой точке.
Тело, ограниченное основной уровенной поверхностью, называют геоидом. Вследствие неравномерного распределения масс внутри Земли поверхность геоида является весьма сложной и не выражается ни одной из рассматриваемых в математике поверхностей. Поэтому возникла необходимость замены поверхности геоида вспомогательной, возможно ближе подходящей к ней поверхности.
- 9 -
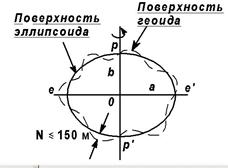
В первом приближении уровенную поверхность Земли можно заменить сферой определенного радиуса. Но, наиболее близкой к геоиду является фигура, образованная вращением эллипса pe'p'e (рис. 2.8) вокруг малой оси pp', называемой полярной осью. В связи с этим возникает необходимость в определении размеров земного эллипсоида, т.е. в определении его параметров: большой полуоси a, малой полуоси b, сжатия 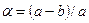 и данных, определяющих положение эллипсоида относительно геоида. Эллипсоид, наиболее близко подходящий к фигуре геоида в целом,
и данных, определяющих положение эллипсоида относительно геоида. Эллипсоид, наиболее близко подходящий к фигуре геоида в целом,  называется общим земным эллипсоидом.
называется общим земным эллипсоидом.
 Эллипсоид, c определенными
Эллипсоид, c определенными
параметрами, ориентирован-
ный в теле Земли и принятый для производства всех карто-графо - геодезических работ
в данной стране, называется референц - эллипсоидом.
В России для производства картографо - геодезических работ принят эллипсоид, определение размеров кото-рого и ориентирование в теле
Рис. 2.8. Общий Земной эллипсоид Земли выполнены под руковод-
ством Ф.Н. Красовского.
Эллипсоид Красовского имеет слеующие размеры:
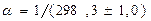 ; a =
; a = 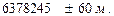
В настоящее время за фигуру Земли принимается тело, ограниченное физической поверхностью Земли, т.е.: на cуше - поверхностью ее твердой оболочки, а на территории океанов и морей - их невозмущенной поверхностью. Изучение фигуры Земли производится путем определения положения точек местности в избранной системе координат на поверхности фигуры относимости, т.е. на поверхности референц-эллипсоида Красовского. Отметим, что при решении многих задач геодезии за фигуру Земли с достаточной для практических целей точностью принимается шар, равновеликий по объёму эллипсоиду Красовского, с радиусом R =6371,11км. Для сравнительно небольших участков земной поверхности в качестве поверхности относимости можно принять горизонтальную плоскость. Горизонтальной называют плоскость, которая нормальна отвесной линии в данной точке поверхности Земли.
- 10 -
2.3. Расчёт размеров участка сферической (уровенной) поверхности Земли для обобщения её до горизонтальной плоскости
Пусть ABD (рис. 2.9) часть уровенной поверхности Земли, принимаемой за сферу с центром c и радиусом R. Обозначим длину дуги ABD через s. Проведем в средней точке B дуги ABD касательную к ней и продолжим радиусы CA и CD до пересечения с касательной в точках A' и D'. Рассчитаем, какая погрешность произойдёт от замены дуги s отрезком касательной A'D' = d. Для этого определим разность
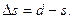 (2.1)
(2.1)
Обозначим центральный угол ACD через ε. Тогда
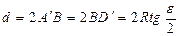 и
и 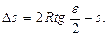 (2.2)
(2.2)
Раскладывая 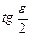 в ряд Маклорена и, ограничиваясь при этом двумя членами разложения, получим
в ряд Маклорена и, ограничиваясь при этом двумя членами разложения, получим
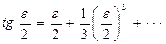 , (2.3)
, (2.3)
где ε - выражено в радианной мере. В свою очередь, как центральный угол
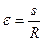 , (2.4)
, (2.4)
поэтому формула (2.3) примет вид
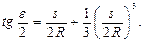 (2.5) Подставив (2.5) в (2.2), получим
(2.5) Подставив (2.5) в (2.2), получим
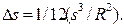 (2.6)
(2.6)
Найдём отношение погрешности Δs к s, которое в геодезии принято называть относительной погрешноcтью.
Будем иметь 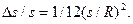 (2.7)
(2.7)
Максимальная точность линейных измерений на поверхности Земли составляет 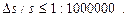 С учетом равенства (2.7)
С учетом равенства (2.7)
вычислим 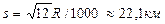 при R = 6371,11 км.
при R = 6371,11 км.
- 11 –
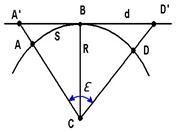
Следовательно, участок сферичес- кой поверхности Земли диаметром 22,1 км, площадью 383,6 км2, можно с практически неощутимой погрешно-стью принять за плоский, а кривизной поверхности Земли в пределах ука-занного участка можно пренебречь.
Рис. 2.9. Влияние кривизны Земли
на горизонтальные расстояния
2.4. Определение положения точек земной поверхности и применяемые для этого в геодезии системы координат
2.4.1. Метод проекций в геодезии. Величины, подлежащие измерению
Физическая поверхность Земли – сочетание различного рода пространственных форм: холмов, котловин, хребтов, лощин, балок, оврагов и т.д. Для изучения такой сложной поверхности в геодезии применяют метод проекций. Так как фигуру Земли в первом приближении принимают за шар, рассмотрим способ проектирования земной поверхности на сферу. Допустим, что поверхности геоида и эллипсоида на некотором участке совпадают, образуя одну уровенную поверхность MN (рис. 2.10,а).
Пространственный многоугольник ABCDEF физической поверхности Земли проектируют на поверхность MN отвесными линиями. Точки a, b, c, d, e, f, в которых отвесные линии пересекают уровенную поверхность MN, называют горизонтальными проекциями соответствующих точек местности, а многоугольник abcdef – горизонтальной проекцией многоугольника ABCDEF. Чтобы по горизонтальной проекции можно было судить о форме пространственного многоугольника, очевидно, необходимо знать величины Aa, Bb, Cc,...,Ff, т.е. расстояния точек местности по отвесным линиям до уровенной поверхности Земли, называемые высотами точек местности. В § 2.3 было показано, что небольшой участок сферической и уровенной поверхностей Земли можно заменить горизонтальной плоскостью, касающейся поверхности в центре этого участка.
- 12 –
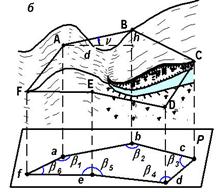
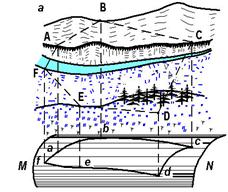
Рис. 2.10. Схемы к методу проекций
Поэтому, если участок местности, заключенный в многоугольнике ABCDEF (см. рис. 2.10,б), имеет небольшие размеры, то при проек-тировании уровенную поверхность заменяют горизонтальной плоскостью P. Линии проектирования Aa,Bb,.., и т.д. перпендику-лярны плоскости P *, стороны ab, bc,...,cf и углы между ними явля-ются горизонтальными проекциями соответствующих сторон и углов местности, а плоский многоугольник abcdef - горизонтальной проекцией многоугольника ABCDEF, расположенного на физической поверхности Земли. Непосредственными измерениями на местности получают: расстояния AB, BC,...,FA, горизонтальные углы β1, β2, β3,…, между ними, превышения h и углы наклона ν линий. От непосредственно измеренной длины линии местности, например 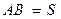 , переходят к длине ее проекции на горизонтальную плоскость
, переходят к длине ее проекции на горизонтальную плоскость 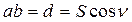 . Длина ортогональной проекции линии местности на горизонтальную плоскость называется горизонтальным проложением этой линии. Углом наклона (вертикальным углом) линии местности называется линейный угол в отвесной плоскости между этой линией и ее проекцией на горизонтальную плоскость. По измеренным превышениям вычисляют высоты точек местности. Например, по известной высоте Aa точки A и превышению h получим высоту
. Длина ортогональной проекции линии местности на горизонтальную плоскость называется горизонтальным проложением этой линии. Углом наклона (вертикальным углом) линии местности называется линейный угол в отвесной плоскости между этой линией и ее проекцией на горизонтальную плоскость. По измеренным превышениям вычисляют высоты точек местности. Например, по известной высоте Aa точки A и превышению h получим высоту 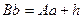 .
.
______________________
- 13 -
2.4.2. Понятия о плане, карте, профиле линии местности
Карта, план - чертежи поверхности Земли, выполненные в той или иной проекции. Планом местности называется уменьшенное и подобное изображение на плоскости (на бумаге, лавсане и пр.) горизонтальной проекции небольшого участка земной поверхности.
Уменьшенное и искаженное, вследствие влияния кривизны Земли, изображение на плоскости горизонтальной проекции значительной части или всей земной поверхности, построенное по определенным математическим законам, называется картой местности.
Карты и планы называются контурными, если на них изображены лишь контуры и предметы местности. Если, кроме перечисленного, изображен и рельеф местности, т.е. совокупность неровностей зем-ной поверхности, то карты и планы называют топографическими. Сечение поверхности Земли отвесной плоскостью, проходящей через концы отрезка линии AB (см. рис. 2.12), называется профилем линии AB местности. Его уменьшенное изображение на бумаге также называется профилем. Отвесной называют плоскость, содержащую отвесную линию.
2.4.3. Астрономические и геодезические координаты.
Высоты точек поверхности Земли
Для определения формы и размеров Земли, изображения поверхности ее на планах и картах необходимо:
1) определить параметры и выполнить ориентирование в теле Земли достаточно простой в геометрическом отношении фигуры относимости - референц-эллипсоида;
2) из результатов геодезических, астрономических и гравимет-рических измерений на поверхности Земли получить величины (координаты), однозначно определяющие положение множества точек поверхности Земли относительно поверхности эллипсоида;
3) по результатам математической обработки материалов геоде-зических измерений определить вид физической поверхности Земли и фигуры Земли в целом.
Положение точки на поверхности Земли определяется ее геогра-фическими координатами: широтой и долготой.
По способу определения географические координаты могут быть астрономическими и геодезическими. Астрономические коорди-наты определяют по данным наблюдений небесных светил, и зависят они от направления отвесной линии в данной точке земной поверхности.
- 14 -
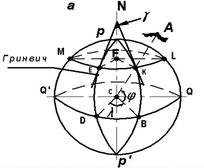
Рис. 2.11. Географические координаты
Примем в качестве фигуры относимости сферу с центром c (см.рис. 2.11,a). PP' -ось вращения Земли. Исходными в указанной системе координат являются плоскость экватора QBDQ' и плоскость начального меридиана PEDP'. Согласно международному согла-шению в России за начальный меридиан принят - Гринвичский *.
Астрономической широтой φ точки K называется угол KCB, образованный отвесной линией KC в точке K с плоскостью QBDQ' небесного экватора (т.е. с плоскостью, перпендикулярной оси вращения Земли). Этот угол измеряется дугой KB меридиана точки K от 0º (на экваторе) до 90º (на полюсе). Широта бывает северная и южная, в зависимости от того, в каком полушарии расположена точка (в северном или южном).
Астрономической долготой λ точки K называется двугранный угол, образованный плоскостями астрономических меридианов данной точки и начального. Плоскостью астрономического меридиана данной точки называется плоскость, проходящая через отвесную линию в этой точке и параллельная оси вращения Земли. Счет долгот ведется от гринвичского меридиана на восток и запад от 0 до 180°. Так, точка K имеет восточную долготу, а точка M – западную.
Геодезические координаты относятся к принятому земному эллипсоиду и определяются в данной точке положением нормали к
поверхности эллипсоида относительно плоскостей экватора и начального меридиана (рис. 2.11,б).
_______________________
* Меридиан, проходящий через центр главного зала Гринвичской обсерватории; Гринвич – округ г. Лондона
- 15 -
Геодезической широтой B точки K называется угол KОB, который образует нормаль KC' с плоскостью экватора.
Геодезической долготой L точки K называется двугранный угол, образованный плоскостями геодезических меридианов данной точки и начального. Плоскостью геодезического меридиана данной точки называется плоскость, содержащая нормаль к поверхности эллипсоида в этой точке и полярную ось PP'. Сечение поверхности эллипсоида этой плоскостью называется геодезическим меридианом. Геодезические меридианы – эллипсы. Сечения поверх-ности эллипсоида плоскостями, перпендикулярными полярной оси - геодезические параллели. Геодезические параллели - окружности. Счет и название геодезических широт аналогичен астрономическим. Счет геодезических долгот ведется от гринвичского меридиана на восток от 0 до 360º. Положение точки на поверхности земного эллипсоида вполне определяется геодезическими координатами: геодезической широтой B и геодезической долготой L. Для определения положения точки A, находящейся на физической поверхности Земли, необходимо знать третью величину – высоту (см. рис. 2.11,б и 2.12).
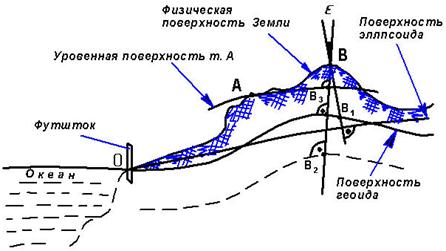
Рис. 2.12. Высоты точек
-16 -
Высоты различают: абсолютные – H = BB1, условные - H' = BB2 и относительные (превышения) – h = BB3. Абсолютной высотой точки земной поверхности называется расстояние ее до основной уровенной поверхности Земли, измеренное по нормали к поверхности эллипсоида. В России и странах СНГ в качестве основной уровенной поверхности принята поверхность, совпадающая со средним уровнем воды Финского залива Балтийского моря. Счет абсолютных высот ведется от ноля Кронштадского футштока*. Система абсолютных высот называется Балтийской. Условной высотой точки земной поверхности называется расстояние этой точки до уровенной поверхности, не совпадающей с основной, измеренное по отвесной линии в данной точке. Превышением h (относительной высотой) точки B над точкой A называется расстояние точки B до уровенной поверхности точки A, измеренное по нормали к этой поверхности. Геодезические измерения по определению высот точек земной поверхности называются нивелированием. Численное выражение высоты точки называетсявысотной отметкой или, просто, отметкой.
2.4.4. Влияние кривизны Земли на определение высот точек
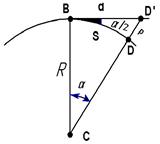 При замене небольшого участка BD (рис. 2.13) уровенной поверх-ности Земли касательной BD' точка D перемещается в D', в связи с чем меняется ее высота на величину p. Величина p выражает влияние кривизны Земли на высоты
При замене небольшого участка BD (рис. 2.13) уровенной поверх-ности Земли касательной BD' точка D перемещается в D', в связи с чем меняется ее высота на величину p. Величина p выражает влияние кривизны Земли на высоты
точек и называется поправкой за кривизну Земли. Определим ее величину. Из прямоугольного треугольника CBD' имеем
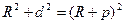 . (2.8)
. (2.8)
Далее получим 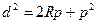 , (2.9)
, (2.9)
Откуда 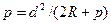 . (2.10)
. (2.10)
Так как p весьма мало по сравнению
с R, то в знаменателе правой части
равенства его можно отбросить. Рис. 2.13. Поправка
за кривизну Земли
 |
* Он представляет собой медную пластину, замурованную в один из устоев моста обводного канала в Кронштадте; нанесенная на пластину черта является нулем футштока. Название образовалось путем соединения английского слова foot (фут) с немецким stock (палка, шест).
- 17 -
Тогда окончательно получим 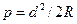 . (2.11)
. (2.11)
Легко подсчитать, что при d = 1 км и R = 6371 км, p = 78,5 мм, а при d = 100 м, p = 0,8 мм. Следует иметь что высоты точек местно-сти часто необходимо знать с точностью до 1,0 мм. Поэтому, даже при коротких расстояниях (50 ÷ 100 м), влияние кривизны Земли на высоты точек необходимо учитывать.
2.4.5. Проекция Гаусса – Крюгера*. Зональная и условная
системы прямоугольных координат на плоскости.
В СССР с 1928 г. для составления топографических карт приме-няется равноугольная (конформная) поперечно-цилиндрическая проекция, предложенная К.Ф. Гауссом. Сущность проекции Гаусса состоит в следующем. Представим, что земной шар вписан в цилиндр (см. рис. 2.14), который касается его по среднему (осевому) меридиану зоны POР'. Ось цилиндра HH' расположена в плоскости экватора Q'OQ и проходит через центр C шара. Плоское изображение каждой зоны получают путём проектирования ее определенным образом на боковую поверхность цилиндра, касающегося осевого меридиана зоны. После чего цилиндр раз-резается по образующей KK' и его боковая поверхность раз-вёртывается в плоскость. При проектировании зоны Гаусс поставил условие, чтобы изображение малого участка на цилиндре было подобно соответствующему участку на сфере; следовательно, углы между соответствующими линиями на шаре и на плоскости равны между собой.
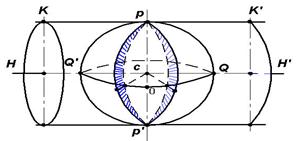
Рис. 2.14. К проекции Гаусса - Крюгера
 |
* Проекция разработана Гауссом в 30-х годах XIX в.; в 1912 г. Крюгер в работе " Конформное изображение земного эллипсоида на плоскости" предложил формулы для вычисления в этой проекции.
- 18 -
Выполнение этого условия приводит к увеличению длин линий на плоскости. Величину искажения ∆ s линий проекции можно вычислить по формуле 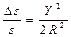 , (2.12)
, (2.12)
где 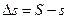 ; s - длина линии на шаре; S - длина проекции линии;
; s - длина линии на шаре; S - длина проекции линии;
Y - расстояние от осевого меридиана зоны до средней точки линии; R - радиус земного шара (R = 6371,11 км).
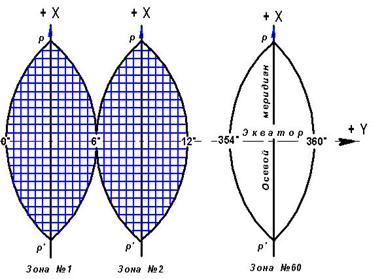
Рис. 2.15. Проекции зон
Для территории СНГ на широтах 36 ≤ φ ≤ 70°, величина линейного искажения на краях зоны меняется от 1 / 1100 до 1/ 6000. Такие величины не превышают графических погрешностей построения карт масштаба 1:10 000, поэтому масштаб изображения на таких и более мелкого масштаба картах в проекции Гаусса остается постоянным. Для планов масштабов 1:5000 и крупнее применяются трехградусные зоны. Счет зон ведется от Гринвичского меридиана на восток. Проектируя последовательно одну зону за другой, получают изображение поверхности земного шара в виде шестидесяти плоских двуугольников (рис. 2.15).
- 19 -
2.4.6. Зональная система плоских прямоугольных координат
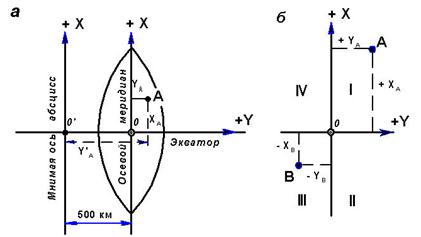 Данная система образуется двумя взаимно перпендикулярными линиями, представляющими изображения осевого меридиана зоны и экватора на плоскости. Изображение осевого меридиана принимается за ось абсцисс с положительным направлением на север. Осью ординат является изображение экватора с положительным направлением на восток.
Данная система образуется двумя взаимно перпендикулярными линиями, представляющими изображения осевого меридиана зоны и экватора на плоскости. Изображение осевого меридиана принимается за ось абсцисс с положительным направлением на север. Осью ординат является изображение экватора с положительным направлением на восток.
Рис. 2.16. Системы прямоугольных координат
Для территории СНГ, расположенной в северном полушарии, абсциссы любых точек положительны. Чтобы сделать положительными и ординаты точек, условились перенести начало счета ординат к западу от осевого меридиана на 500 км (см. рис. 2.16). Эти ординаты называются преобразованными. Номер зоны, к которой относятся координаты, указывается перед численным значением преобразованной ординаты. Например, точка с координатами X = 6015,76 и Y = 9652,66 км находится в зоне №9 на расстоянии 152,66 км к востоку от осевого меридиана этой зоны.
2.4.7. Условная система прямоугольных координат на плоскости
Для инженерно-геодезических работ, выполняемых на небольших площадях, применяют условную систему прямоугольных координат (рис. 2.16, б).
- 20 -
Ось абсцисс (оX) такой системы совмещают с меридианом некоторой (обычно крайней юго-западной) точки участка, либо располагают параллельно основным осям сооружений. Положительное направление оси абсцисс (oX) выбирают на север (на чертеже - вверх), оси ординат (oY) - на восток (на чертеже - вправо). Применяемая в геодезии система прямоугольных координат называется левой. В ней поворот от оси oX к оси oY (на наименьший угол) до их совмещения осуществляется по движению часовой стрелки.
 2014-02-02
2014-02-02 3329
3329








