Геометрическая интерпретация задач дает возможность наглядно представить их структуру, выявить особенности. Задачу линейного программирования с двумя переменными всегда можно решить графически. Однако уже в трехмерном пространстве такое решение усложняется, а в пространствах, размерность которых больше трех, графическое решение, вообще говоря, невозможно.
Рассмотрим случай двух переменных:
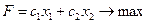 (5)
(5)

Дадим геометрическую интерпретацию элементов этой задачи.
Каждое из ограничений (6), (7) задаёт на плоскости x1Ox2 некоторую полуплоскость. Полуплоскость – выпуклое множество. Напомним, что выпуклым называют множество, которое вместе с любыми своими точками x1 и x2 содержит и все точки отрезка [ x1; x2 ]. Пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений (ОДР) задачи есть выпуклое множество.
Возможны ситуации, когда область допустимых решений ЗЛП:
- выпуклый многоугольник;
- неограниченная выпуклая многоугольная область;
- единственная точка;
- прямая линия;
- луч;
- отрезок;
- пустое множество.
Геометрическая интерпретация целевой функции.
Пусть ОДР задачи ЛП – непустое множество.
Выберем произвольное значение целевой функции 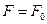 , получим
, получим 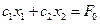 . Это уравнение прямой линии. В точках прямой целевая функция сохраняет одно и то же постоянное значение
. Это уравнение прямой линии. В точках прямой целевая функция сохраняет одно и то же постоянное значение 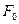 . Считая в равенстве
. Считая в равенстве 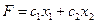
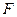 параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции. Найдем частные производные целевой функции по x1 и x2:
параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции. Найдем частные производные целевой функции по x1 и x2: 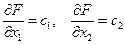 .
.
Частная производная функции показывает скорость её возрастания вдоль данной оси. с1 и с2 – скорости возрастания 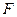 соответственно вдоль осей Ox1 и Ox2. Вектор
соответственно вдоль осей Ox1 и Ox2. Вектор 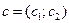 называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции. Вектор
называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции. Вектор 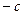 указывает направление наискорейшего убывания целевой функции Его называют антиградиентом.
указывает направление наискорейшего убывания целевой функции Его называют антиградиентом.
Вектор 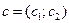 перпендикулярен к прямой
перпендикулярен к прямой 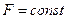 семейства
семейства 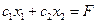 .
.
Из геометрической интерпретации элементов ЗЛП вытекает следующий порядок её графического решения.
1. С учетом системы ограничений строится область допустимых решений.
2. Строится вектор 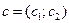 .
.
3. Проводится произвольная линия, перпендикулярная к вектору 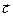 .
.
4. При решении задачи на максимум перемещается линия уровня в направлении вектора 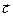 так, чтобы она касалась области допустимых решений в ее крайнем положении.
так, чтобы она касалась области допустимых решений в ее крайнем положении.
В случае задачи на минимум линия уровня перемещается в антиградиентном направлении.
5. Определяется оптимальный план 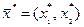 и экстремальное значение целевой функции
и экстремальное значение целевой функции 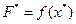 .
.
Возможны следующие случаи:
- оптимальный план единственный;
- оптимальных планов бесконечное множество: в разрешающем положении линия уровня проходит через сторону области допустимых решений;
- целевая функция неограниченна;
- область допустимых решений состоит из единственной точки, где целевая функция достигает одновременно и максимального и минимального значения;
- задача не имеет решения: ОДР – пустое множество, т.е. система ограничений задачи несовместна.
Пример. Пусть предприятие изготавливает изделия двух видов А и В. Для производства изделий оно располагает сырьевыми ресурсами 3-х видов С, D и E в объёмах 600, 480 и 240 единиц соответственно. Нормы расхода ресурсов на единицу продукции каждого вида известны и даны в таблице 1. Прибыль от реализации изделия А составляет 40 млн. руб., а изделия В- 50 млн. руб. Требуется найти объёмы производства изделий, обеспечивающие максимальную прибыль.
Таблица 1
| А | В | |
| С | ||
| D | ||
| E |
Решение. Построим математическую модель задачи.
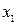 - количество деталей A,
- количество деталей A,
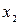 - количество деталей B,
- количество деталей B,
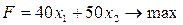
Ограничения будут иметь вид:
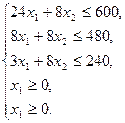
Решение сформулированной задачи найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений-неравенств запишем в виде уравнений и пронумеруем их:
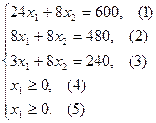
Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.
Чтобы построить первую прямую, найдем точки её пересечения с осями координат: при x1 = 0, х2 = 75, а при х2 = 0, x1 = 25. Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем точку 0(0,0) и подставим ее координаты в неравенство — оно удовлетворяется. Так как точка 0(0,0) лежит левее первой прямой, то и полуплоскость будет находиться левее прямой 24 х1 + 8 х2 = 600. На рис. 1 расположение полуплоскости относительно первой прямой отмечено стрелками.
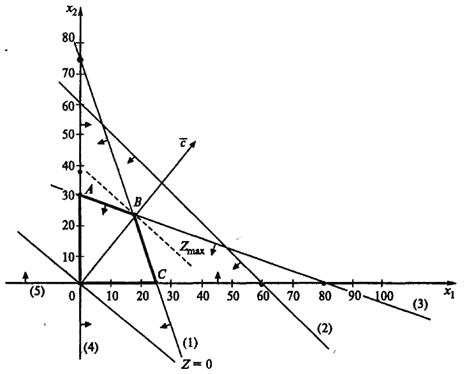
Рис. 1
Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенствам. Точки, удовлетворяющие ограничениям х1, ³ 0, х2 ³ 0, находятся в первом квадранте.
Множество точек, удовлетворяющих всем ограничениям одновременно, является ОДР системы ограничений. На графике (рис. 1) это многоугольник ОАВС.
Любая точка многоугольника решений удовлетворяет системе ограничений задачи и, следовательно, является ее решением. Это говорит о том, что данная задача линейной оптимизации имеет множество допустимых решений, т.е. многовариантна. Нам же необходимо найти решение, обеспечивающее максимальную прибыль.
Приравняем функцию к нулю и построим соответствующую прямую. Вектор-градиент прямой функции 40 х1 + 50 х2 = 0 имеет координаты 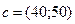 . Изобразим вектор на графике и построим прямую перпендикулярно этому вектору (рис. 1). Перемещая прямую функции параллельно самой себе в направлении вектора, увидим, что последней точкой многоугольника решений, которую пересечет прямая функции, является угловая точка В. Следовательно, в точке В функция достигает максимального значения.
. Изобразим вектор на графике и построим прямую перпендикулярно этому вектору (рис. 1). Перемещая прямую функции параллельно самой себе в направлении вектора, увидим, что последней точкой многоугольника решений, которую пересечет прямая функции, является угловая точка В. Следовательно, в точке В функция достигает максимального значения.
Координаты точки В найдем, решая систему уравнений, прямые которых пересекаются в данной точке:
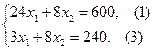
Решив эту систему, получим, что х1 = 17,14; х2 = 23, 57. Следовательно, если предприятие изготовит изделия в найденных объемах, то получит максимальную прибыль, равную
Zmax = 40×17,14 + 50×23,57 = 1 864,1(млн. руб.).
 2014-02-02
2014-02-02 20556
20556
